In band theory of solids we understand the energy level structures of solid. The energy levels of the overlapping electron shells are all slightly altered.
The energy differences are very small, but enough so that a large number of electrons can be in close proximity and still satisfy the Pauli exclusion principle.
The result is the formation of energy bands, consisting of many states close together but slightly split in energy.
A detailed analysis of energy bands shows that there are as many separate energy levels in each band as there are atoms in a crystal.
Suppose there are N atoms in a crystal. Two electrons can occupy each energy level (spin), so there are 2N possible quantum states in each band.
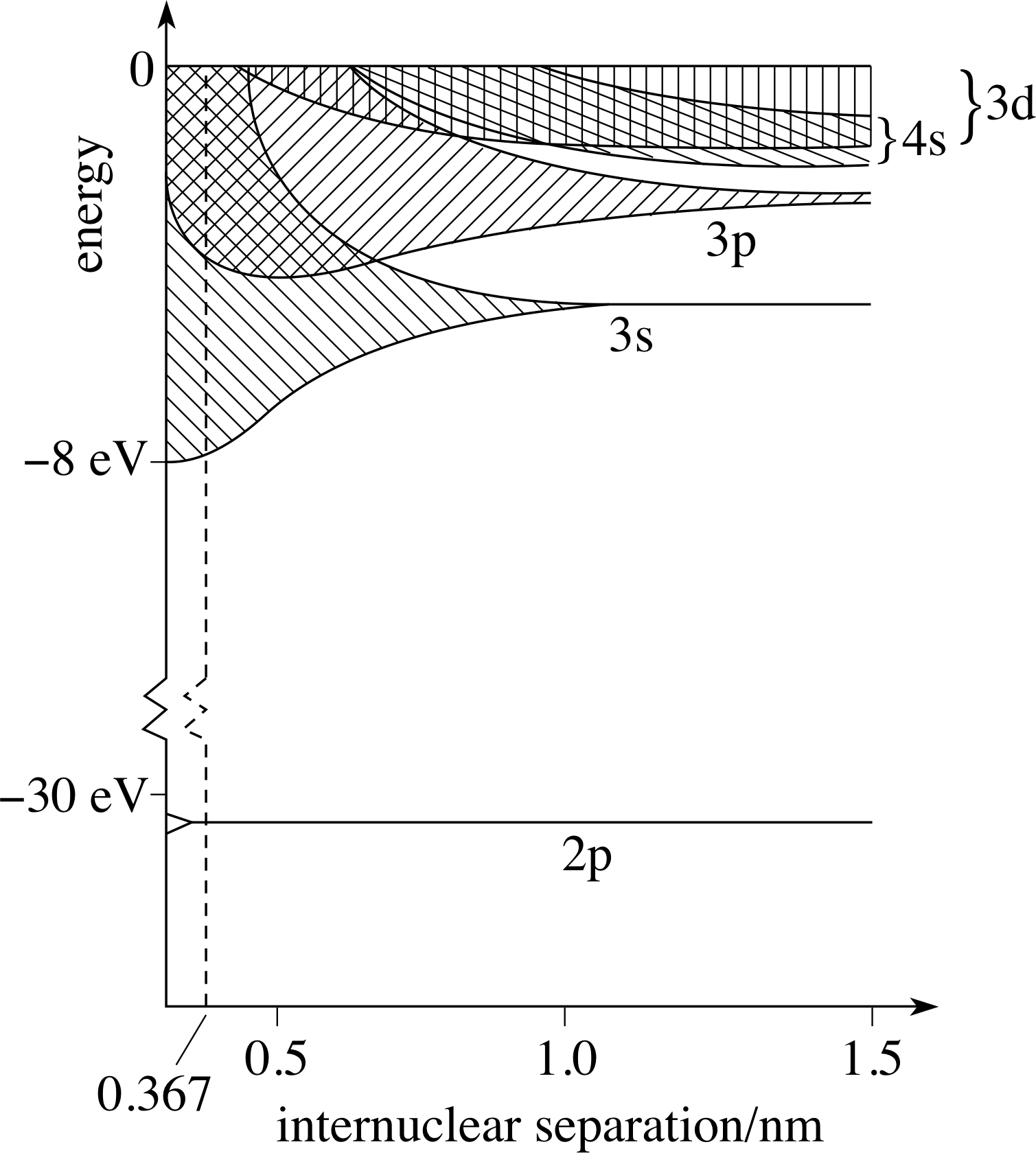
Let’s consider sodium as an example. Sodium has a single outer 3s electron.
When you bring two sodium atoms together, the 3s energy level splits into two separate energy levels.
Things to note: 4 quantum states but only 2 electrons.
You could minimize electron energy by putting both 3s electrons in the lower energy level, one spin up and the other spin down.
There is an internuclear separation which minimizes electron energy. If you bring the nuclei closer together, energy increases.
When you bring five sodium atoms together, the 3s energy level splits into five separate energy levels.
The three new energy levels fall in between the two for 2 sodiums.
There are now 5 electrons occupying these energy levels.
I’ve suggested one possible minimum-energy configuration. Notice how the sodium-sodium internuclear distance must increase slightly.
There are now N electrons occupying this 3s band. They go into the lowest energy levels they can find. The shaded area represents available states, not filled states. At the selected separation, these are the available states.
As an aid to visualization, we often represent energy bands like this
(using sodium as an example):
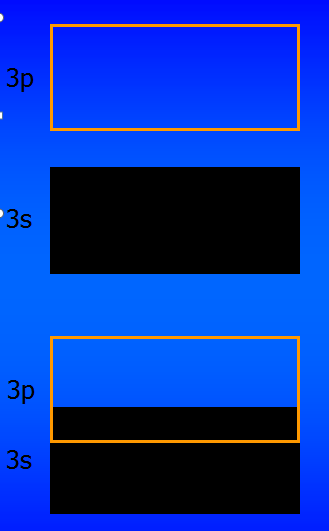
Sodium has a single 3s electron, so the 3s energy band contains twice as many states as there are electrons. The band is half full.
At T=0 the band is filled exactly halfway up, and the Fermi level, εF, is right in the middle of the band.
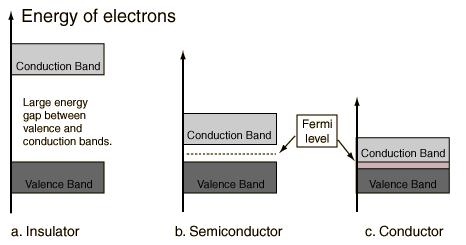
Sodium is a metal because an applied field can easily give energy to and accelerate an electron.
Magnesium has two 3s electrons. You expect the 3s band to be full, the 3p band to be empty, with a forbidden gap in between. Magnesium should be an insulator. (Why?)
But magnesium is a metal (actually, a “semimetal”).
The 3p and 3s bands overlap. There are many empty states nearby into which electrons can be accelerated.
Materials which have bands either completely full or completely empty are insulators (unless band overlap occurs, as was the case for magnesium).
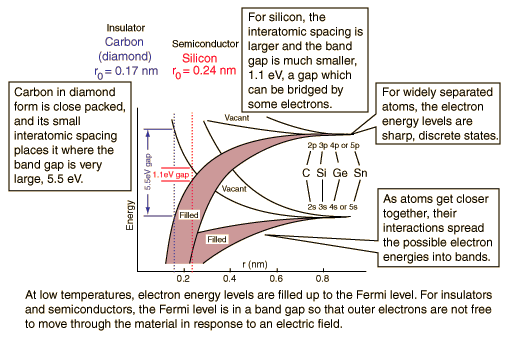
In a carbon atom, the 2p shell contains 2 electrons. There are 6 available states, so one would expect the 2p band to be 1/3 full* and carbon to be a conductor.
But carbon is an insulator. Why?
A semiconductor is a material which has a filled (at T=0) valence band separated by a small gap from an empty (at T=0) conduction band.
A semiconductor (Silicon) is a material which has a filled (at T=0) valence band separated by a small gap from an empty (at T=0) conduction band.
References :
web.mst.edu/~pringle/Phys107/Lecture/lect33.ppt
hyperphysics.phy-astr.gsu.edu/hbase/solids/band.html