Co-efficient of friction, Angle of friction, Angle of limiting friction, Angle of repose, Cone of friction for Btech first year

Co-efficient of friction:

The magnitude of the limiting friction bears a constant ratio to the normal reaction between the two surfaces of contact and this ratio is called coefficient of friction.

Coefficient of friction, µ = F/N

Where F = Force of friction

               N = Normal reaction

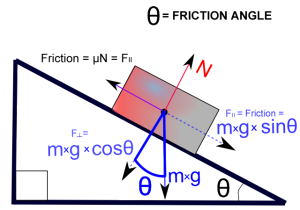
Angle of friction:

At the contact surface, two reaction force of friction “F” and normal reaction “N” acts and combined graphically to get the reaction “R” which acts at angle “θ” called angle of friction.

tan θ = F/N = µ

Angle of limiting friction:

The angle between the resultant reaction and the normal reaction to the plane on which the motion of the body is impending.

tan α = F/N = µ

Angle of repose:

The maximum inclination of the plane on which a body, free from external forces, can repose is called angle of repose.

tan ø = F/N

Cone of friction:

The inverted cone with semi central angle “α” equal to limiting frictional angle “α”, is called cone of friction.

Engineers often refer to either the coefficient of friction or the angle of friction. This section describes their relationship and goes on to explain the Cone of friction:

Let R be the normal reaction at a point of contact O and F the frictional force acting in a direction perpendicular to R. Then the total force at O is given by

                                              (2)

acting in a direction making an angle

                                           (3)

with the normal reaction.If friction is limiting, and the action at O makes an angle of with the normal reaction. This angle is denoted by .Thus

                                            (4)

and the magnitude of the limiting friction can be found if either or is known.If the direction in which the body tends to move is varied the the force of limiting friction will always lie in the plane through O perpendicular to the normal reaction and the direction of the total action at O will always lie 0n a cone with it’s vertex at O and axis along the line of the normal reaction. The semi vertical angle will be

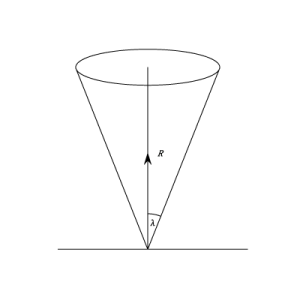
This cone is called the cone of friction. If friction is not limiting, the angle made by the total action at O will be less than. Hence whether the friction be limiting or not, the direction of the total action at O must be inside or on the cone of friction. It follows that if P is the resultant of the other forces acting on the body which is in equilibrium, the direction of P must lie inside or on the cone o friction, since P must balance the total action at O

Feedback is important to us.