D’Alembert’s Principle of Inertial Forces and Dynamic Equilibrium Notes pdf ppt

D’Alembert’s Principle:

The principle states that the sum of the differences between the forces acting on a system of mass particles and the time derivatives of the momenta of the system itself along any virtual displacement consistent with the constraints of the system, is zero. Thus, in symbols d’Alembert’s principle is written as following,

where,

D’Alembert’s Principle of Inertial Forces:

D’Alembert showed that one can transform an accelerating rigid body into an equivalent static system by adding the so-called “inertial force” and “inertial torque” or moment. The inertial force must act through the center of mass and the inertial torque can act anywhere.

The system can then be analyzed exactly as a static system subjected to this “inertial force and moment” and the external forces. The advantage is that, in the equivalent static system one can take moments about any point (not just the center of mass). This often leads to simpler calculations because any force (in turn) can be eliminated from the moment equations by choosing the appropriate point about which to apply the moment equation (sum of moments = zero).

Even in the course of Fundamentals of Dynamics and Kinematics of machines, this principle helps in analyzing the forces that act on a link of a mechanism when it is in motion. In textbooks of engineering dynamics this is sometimes referred to as d’Alembert’s principle.

Example for 1D Motion of a Rigid Body:

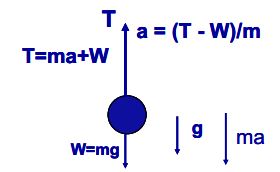
To illustrate the concept of d’Alembert’s principle, let’s use a simple model with a weight , suspended from a wire. The weight is subjected to a gravitational force, , and a tension force in the wire. The mass accelerates upward with an acceleration . Newton’s Second Law becomes or . As an observer with feet planted firmly on the ground, we see that the force accelerates the weight, , but, if we are moving with the wire we don’t see the acceleration, we feel it. The tension in the wire seems to counteract an acceleration “force” .

Example for Plane 2D Motion of a Rigid Body:

For a planar rigid body, moving in the plane of the body (the x–y plane), and subjected to forces and torques causing rotation only in this plane, the inertial force is

where is the position vector of the centre of mass of the body, and is the mass of the body. The inertial torque (or moment) is

where is the moment of inertia of the body. If, in addition to the external forces and torques acting on the body, the inertia force acting through the center of mass is added and the inertial torque is added (acting around the centre of mass is as good as anywhere) the system is equivalent to one in static equilibrium. Thus the equations of static equilibrium

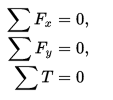
hold. The important thing is that is the sum of torques (or moments, including the inertial moment and the moment of the inertial force) taken about any point. The direct application of Newton’s laws requires that the angular acceleration equation be applied only about the center of mass.

Dynamic Equilibrium:

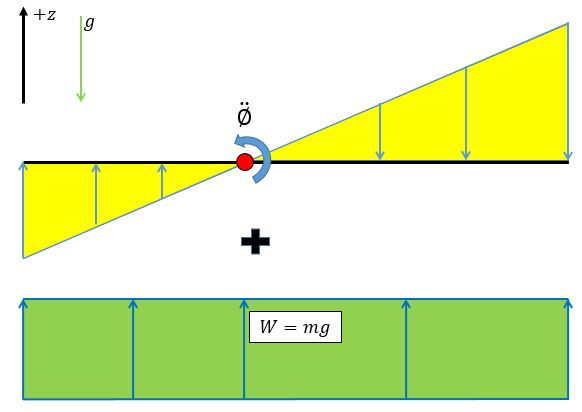
D’Alembert’s form of the principle of virtual work states that a system of rigid bodies is in dynamic equilibrium when the virtual work of the sum of the applied forces and the inertial forces is zero for any virtual displacement of the system. Thus, dynamic equilibrium of a system of n rigid bodies with m generalized coordinates requires that is to be

for any set of virtual displacements δq_j. This condition yields m equations,

which can also be written as

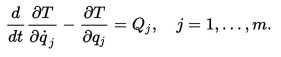
The result is a set of m equations of motion that define the dynamics of the rigid body system.

 

Feedback is important to us.