Plane Motion:
If all moment of a particle occurs in a plane, it is called plane motion of the particle.
General Planar Motion:
General planar motion allows for simultaneous rotational and translational motion in a 2-D plane. The motion of the rigid body may be described as a simple superposition of the body’s translation and rotation as illustrated in the following figure.
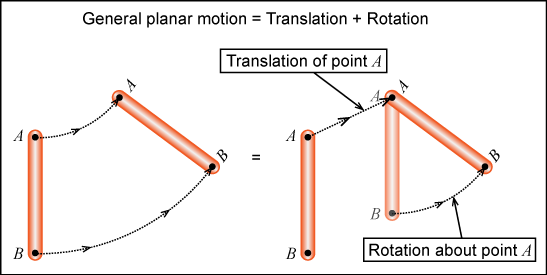
Rectilinear Motion:
If the path of the motion of a particle is a straight line, it is called ‘Rectilinear motion.

Rectilinear motion is another name for straight-line motion. This type of motion describes the movement of a particle or a body.
A body is said to experience rectilinear motion if any two particles of the body travel the same distance along two parallel straight lines. The figures below illustrate rectilinear motion for a particle and body.
Rectilinear motion for a particle:
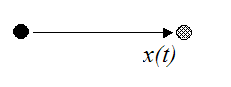
Rectilinear motion for a body:
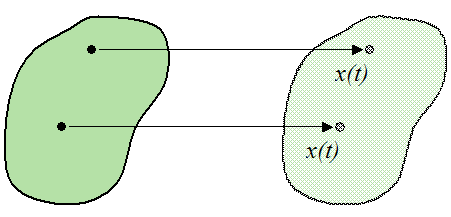
Expression for Rectilinear Motion:
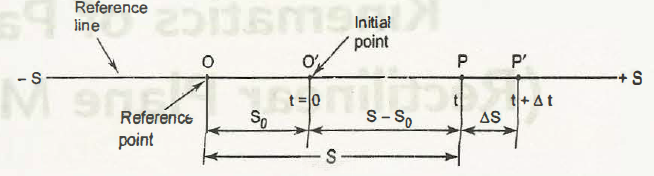
Above Fig. shows the movement of a particle r moving along a straight line. O’ is the initial position of Pat t = 0 and S =S0.
P is the position at time t and P’ is the position at time t+ ∆t
Displacement in time ∆t =∆S
Displacement m unit time =∆S /∆t
∆S /∆t =v av [Average Velocity].
In the limiting case as ∆t à 0, we have
v = Lt .∆S /∆t= dS /dt ,
where v is called instantaneous velocity.
v = dS/dt =S
v = v o at t =0 (i.e., at initial point 0,
The average acceleration during ∆t is defined as
a av =∆v / ∆t.
In the limiting case
where a is called the instantaneous acceleration of the particle.
a = dv /dt =v
-a is called instantaneous deceleration or retardation
Thus , a d2S / dt = S
From (1.1) dt = dS /v
and from (1.2) we have
dt = dv / a.
thus , dt = dS /v = dv /a
v dv =a dS
