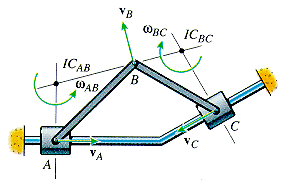
Instantaneous Center of Zero Velocity Notes pdf ppt

Instantaneous Center of Zero Velocity:

For any body undergoing planar motion, there always exists a point in the plane of motion at which the velocity is instantaneously zero (if it were rigidly connected to the body). This point is called the instantaneous center of zero velocity, or IC.

It may or may not lie on the body! If the location of this point can be determined, the velocity analysis can be simplified because the body appears to rotate about this point at that instant.

This point generally does not have zero acceleration and will change locations with time.

Let the instantaneous center be located at point C, that is v_C = 0. Relative velocity says that we can relate the velocity of any other point to the velocity of point C. Therefore, we can write

for point A and

for point B.

From the definition of cross products, we can see that point C must lie on a line through point A that is perpendicular to v_A. The same must also be true for v_B.

1. If v_A and v_B are not parallel, then the instantaneous center of zero velocity will be at the point of intersection of the two perpendicular lines.

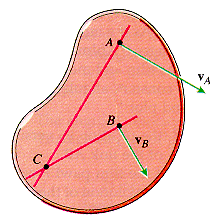
2. If v_A and v_B are parallel and in opposite directions, then the instantaneous center of zero velocity is along the line joining the two points.

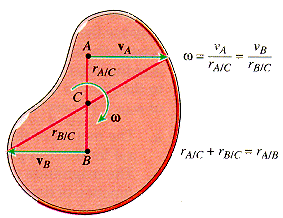
3. If v_A and v_B are parallel and in the same direction, then the instantaneous center of zero velocity is along the line joining the two points, with both points on the same side of the instantaneous center.

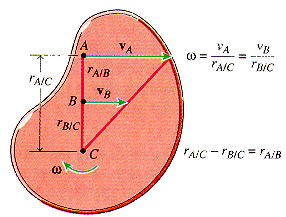
4. If v_A and v_B are equal, then the body is instantaneously in translation and = 0. In this case, one can consider the instantaneous center to be located at infinity.

 

Once the instantaneous center is located, the velocity of any other point in the body can be determined using relative velocity.

When two or more bodies are pinning together, a different instantaneous center can be found for each body. Since the velocity of the point joining two bodies is the same for each body, the instantaneous center of both bodies must lie on a single line through the common point.

Consider the special case of a wheel (or gear) rolling without slip,

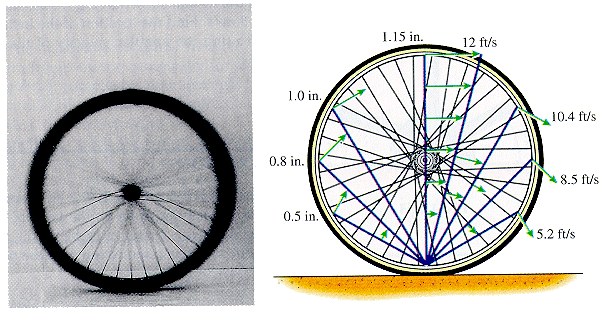
Notice that the instantaneous center is located where the wheel contacts the ground (a stationary object).

Feedback is important to us.