Definition of the linear impulse of a force:
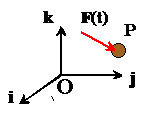
In most dynamic problems, particles are subjected to forces that vary with time. We can write this mathematically by saying that the force is a vector valued function of time 
.
If we express, the force as components in a fixed basis 
, then
where each component of the force is a function of time.
The Linear Impulse exerted by a force during a time interval 
is defined as
The linear impulse is a vector, and can be expressed as components in a basis
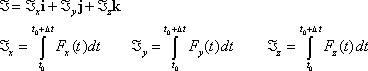
If you know the force as a function of time, you can calculate its impulse using simple calculus. For example:
- For a constant force, with vector value
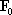the impulse is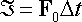 
- For a harmonic force of the form
the impulse is
It is rather rare in practice to have to calculate the impulse of a force from its time variation.
Definition of the linear momentum of a particle:
The linear momentum of a particle is simply the product of its mass and velocity
The linear momentum is a vector 
its direction is parallel to the velocity of the particle.
Impulse-momentum relations for a single particle:
- Consider a particle that is subjected to a force
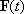
for a time interval 
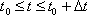
. - Let
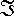
denote the impulse exerted by F on the particle - Let
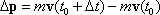
denote the change in linear momentum during the time interval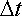 
.
The momentum conservation equation can be expressed either in differential or integral form.
In differential form:
In integral form:
This is the integral of Newton’s law of motion with respect to time.
The impulse-momentum relations for a single particle are useful if you need to calculate the change in velocity of an object that is subjected to a prescribed force
Impulse-momentum relation for a system of particles:
Suppose we are interested in calculating the motion of several particles, sketched in the figure.
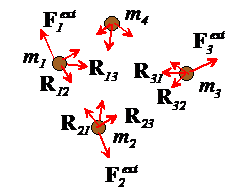
Total external impulse on a system of particles:
Each particle in the system can experience forces applied by:
Other particles in the system (e.g. due to gravity, electric charges on the particles, or because the particles are physically connected through springs, or because the particles collide). We call these internal forces acting in the system. We will denote the internal force exerted by the ith particle on the jth particle by 
.
Note that, because every action has an equal and opposite reaction, the force exerted on the jth particle by the ith particle must be equal and opposite, to 
, i.e. 
.
Forces exerted on the particles by the outside world (e.g. by externally applied gravitational or electromagnetic fields, or because the particles are connected to the outside world through mechanical linkages or springs). We call these external forces acting on the system, and we will denote the external force on the i th particle by 
We define the total impulse exerted on the system during a time interval 
as the sum of all the impulses on all the particles. It’s easy to see that the total impulse due to the internal forces is zero because the ith and jth particles must exert equal and opposite impulses on one another, and when you add them up they cancel out. So the total impulse on the system is simply
Total linear momentum of a system of particles:
The total linear momentum of a system of particles is simply the sum of the momenta of all the particles, i.e.
The impulse-momentum equation can be expressed either in differential or integral form, just as for a single particle:
- In differential form
2. In integral form
This is the integral of Newton’s law of motion with respect to time.
Conservation of momentum:
If no external forces act on a system of particles, their total linear momentum is conserved, i.e. 
.
