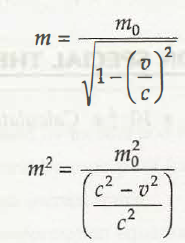Mass Energy Equivalence Notes for Engineering Physics:
Below explained equation gives the universal Mass Energy equivalence. This is another major contribution of Einstein. It signifies the manifestation of energy into the matter and vice-versa. Relativity shows that mass is not any independent quantity, however, it is a form of energy. Its experimental evidences are well known in nuclear fission and fusion reactions.
According to classical mechanics, force F is given by the time derivative of the product of mass (m) and velocity (v), i.e., momentum of the body, and is given by
f = d /dt (mv)
However, according to the theory of relativity, both m and v are variable
So , f d/dt (mv) =mdv/dt +v dm/dt
When a particle is displaced through a distance ‘dx’ on application of a force F, then the
increase in kinetic energy is given by,
dk =f x dx
= [m dv/dt +v dm/dt ] x dx/dt x dt
= [m dv /dt +v dm/dt] x v x dt
Dk =v2 dm +mv dv
Now, we know that
m2 = m02 c2 /c2 –v2
M2 c2 -m2v2 = m02 c2
On differentiation both sides, we get,
2m x dm x c2– [2m x dm x v2 + 2v x dv x m2] = 0
ð 2 m x dm x c2 = 2m [ dm x v2 + v x m x dv]
c2 dm = v2 dm + v m dv
By comparing equations (2) and (3), we have,
D K = c2 d m … (4)
Now, we can consider that the body initially at rest and on application of force it acquires a velocity v. Also the mass of the body increases from m0 tom. Thereby, the total kinetic energy acquired by the body is given by.
ʃ dk = ʃ m mo c2 dm
k =c2 (m m0)
This is the increase in kinetic energy due to the increase in mass.
Now, the total energy of a moving body is the total of kinetic energy due to motion and the energy at rest.
So, E = k + m0 c2 = c2 (m- m0) + m0 c2 = m c2
Hence, [E=m c2 ]
The conversion of mass and energy and the reverse are also illustrated in nature itself. When a particle collides with an anti-particle there is a mutual annihilation and the total mass is converted into radiant energy. Thus, the conservation of mass takes place into energy. Other way, when a radiant energy comes near a charged nucleus, particle and anti-particle are created. Thus the energy is converted into mass.