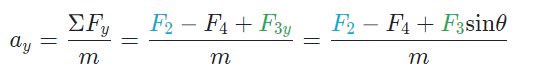Newton’s Second Law of Motion:
The second law states that the acceleration of an object is dependent upon two variables – the net force acting upon the object and the mass of the object. The acceleration of an object depends directly upon the net force acting upon the object, and inversely upon the mass of the object. As the force acting upon an object is increased, the acceleration of the object is increased. As the mass of an object is increased, the acceleration of the object is decreased.
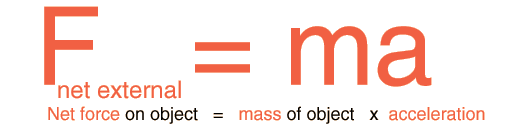
What is Newton’s second Law?
We know objects can only accelerate if there are forces on the object. Newton’s second law tells us exactly how much an object will accelerate for a given net force.
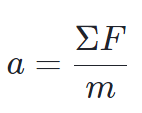
To be clear, a is the acceleration of the object, ΣF is the net force on the object, and m is the mass of the object.
Looking at the form of Newton’s second law shown above, we see that the acceleration is proportional to the net force, ΣF, and is inversely proportional to the mass, m. In other words, if the net force were doubled, the acceleration of the object would be twice as large. Similarly, if the mass of the object were doubled, its acceleration would be half as large.
What does net force mean?
A force is a push or a pull, and the net force ΣF is the total force—or sum of the forces—exerted on an object. Adding vectors is a little different from adding regular numbers. When adding vectors, we must take their direction into account. The net force is the vector sum of all the forces exerted on an object.
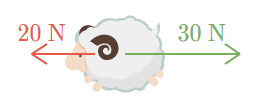
For instance, consider the two forces of magnitude 30 N and 20 N that are exerted to the right and left respectively on the sheep shown above. If we assume rightward is the positive direction, the net force on the sheep can be found by

If there were more horizontal forces, we could find the net force by adding up all the forces to the right and subtracting all the forces to the left.
Since force is a vector, we can write Newton’s second law as 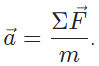
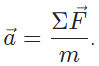
This shows that the direction of the total acceleration vector points in the same direction as the net force vector. In other words, if the net force ΣF points right, the acceleration a must point right.
How do We use Newton’s second law?
If the problem you’re analyzing has many forces in many directions, it’s often easier to analyze each direction independently.
In other words, for the horizontal direction we can write
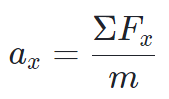
This shows that the acceleration 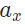 , in the horizontal direction is equal to the net force in the horizontal direction, ΣFx, divided by the mass.
, in the horizontal direction is equal to the net force in the horizontal direction, ΣFx, divided by the mass.
Similarly, for the vertical direction we can write
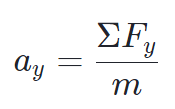
This shows that the acceleration 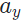 in the vertical direction is equal to the net force in the vertical direction, ΣFy, divided by the mass.
in the vertical direction is equal to the net force in the vertical direction, ΣFy, divided by the mass.
When using these equations we must be careful to only plug horizontal forces into the horizontal form of Newton’s second law and to plug vertical forces into the vertical form of Newton’s second law.
We do this because horizontal forces only affect the horizontal acceleration and vertical forces only affect the vertical acceleration. For instance, consider a hen of mass mmm that has forces of magnitude F1, F2, F3, F4, exerted on it in the directions shown below
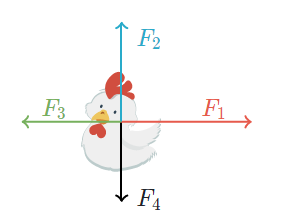
The forces F1 and F3 affect the horizontal acceleration since they lie along the horizontal direction. Applying Newton’s second law to the horizontal direction and assuming rightward is positive, we get
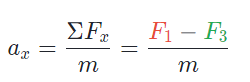
Similarly, the forces F2 and F4 affect the vertical acceleration since they lie along the vertical direction. Applying Newton’s second law to the vertical direction and assuming upward is positive, we get
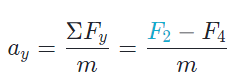
What do we do when a force is directed at an angle?
When forces are directed in diagonal directions, we can still analyze the forces in each direction independently. But, diagonal forces will contribute to the acceleration in both the vertical and horizontal directions.
For instance, let’s say the force F3 on the hen is now directed at an angle θ as seen below.
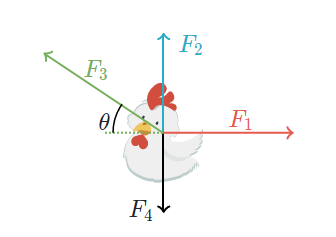
The force F3 will affect both the horizontal and vertical accelerations, but only the horizontal component of F3 will affect horizontal acceleration; only the vertical component of F3 will affect the vertical acceleration. So we’ll break the force F3 into horizontal and vertical components as seen below.
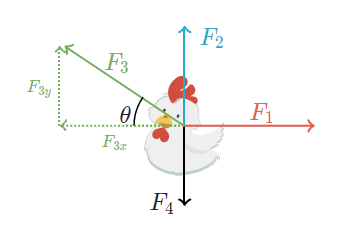
Now we see that the force F3 can be viewed as consisting of a horizontal force F3x and a vertical force F3y .
Using trigonometry, we can find the magnitude of the horizontal component with F3x=F3cosθ .
Similarly, we can find the magnitude of the vertical component with F3y=F3sinθ.
Now we can proceed as usual by plugging all horizontally directed forces into the horizontal form of Newton’s second law.
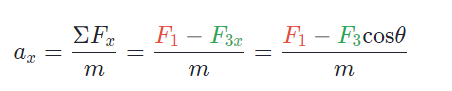
Similarly, we can plug all vertically directed forces into the vertical form of Newton’s second law.