A particle in a 1-dimensional box is a fundamental quantum mechanical approximation describing the translational motion of a single particle confined inside an infinitely deep well from which itcannot escape.
Introduction
The particle in a box problem is a common application of a quantum mechanical model to a simplified system consisting of a particle moving horizontally within an infinitely deep well from which it cannot escape. The solutions to the problem give possible values of E and ψ that the particle can possess. E represents allowed energy values and ψ(x) is a wavefunction, which when squared gives us the probability of locating the particle at a certain position within the box at a given energy level.
To solve the problem for a particle in a 1-dimensional box, we must follow our Big, Big recipe for Quantum Mechanics:
- Define the Potential Energy, V
- Solve the Schrödinger Equation
- Define the wavefunction
- Define the allowed energies
Step 1: Define the Potential Energy V
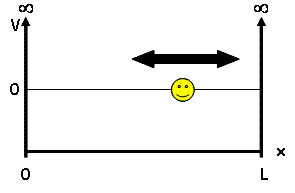
The potential energy is 0 inside the box (V=0 for 0<x<L) and goes to infinity at the walls of the box (V=∞ for x<0 or x>L). We assume the walls have infinite potential energy to ensure that the particle has zero probability of being at the walls or outside the box. Doing so significantly simplifies our later mathematical calculations as we employ these boundary conditions when solving the Schrödinger Equation.

Plsz unlock the content as its very useful during time of semister exam.. This site would be more helpful if excess with Full content is allowed