At the beginning of the twentieth century, experimental evidence suggested that atomic particles were also wave-like in nature. For example, electrons were found to give diffraction patterns when passed through a double slit in a similar way to light waves. Therefore, it was reasonable to assume that a wave equation could explain the behavior of atomic particles.
Schrodinger was the first person to write down such a wave equation. Much discussion then centered on what the equation meant. The eigenvalues of the wave equation were shown to be equal to the energy levels of the quantum mechanical system, and the best test of the equation was when it was used to solve for the energy levels of the Hydrogen atom, and the energy levels were found to be in accord with Rydberg’s Law.
It was initially much less obvious what the wave function of the equation was. After much debate, the wave function is now accepted to be a probability distribution. The Schrodinger equation is used to find the allowed energy levels of quantum mechanical systems (such as atoms, or transistors). The associated wave function gives the probability of finding the particle at a certain position.
The Schrodinger equation is:
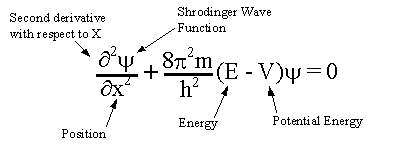
The solution to this equation is a wave that describes the quantum aspects of a system. However, physically interpreting the wave is one of the main philosophical problems of quantum mechanics.
The solution to the equation is based on the method of Eigen Values devised by Fourier. This is where any mathematical function is expressed as the sum of an infinite series of other periodic functions. The trick is to find the correct functions that have the right amplitudes so that when added together by superposition they give the desired solution.
So, the solution to Schrodinger’s equation, the wave function for the system, was replaced by the wave functions of the individual series, natural harmonics of each other, an infinite series. Schrodinger has discovered that the replacement waves described the individual states of the quantum system and their amplitudes gave the relative importance of that state to the whole system.
Schrodinger’s equation shows all of the wave like properties of matter and was one of greatest achievements of 20th century science.
It is used in physics and most of chemistry to deal with problems about the atomic structure of matter. It is an extremely powerful mathematical tool and the whole basis of wave mechanics.
