Diffraction from a single slit gives a characteristic pattern. It also complicates the pattern from Young’s experiment. Here we use phasor addition to derive the intensity as a function of angle for both situations.
Diffraction pattern from a single slit:
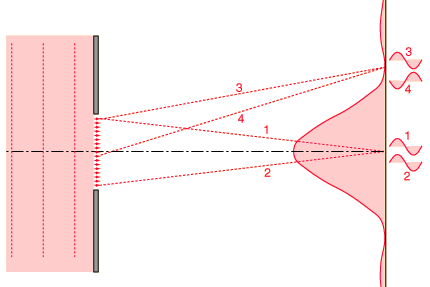
If light from symmetric elements near each edge of the slit travels to the centerline of the slit, as indicated by rays 1 and 2 above, their light arrives in phase and experiences constructive interference.
The first minimum in intensity for the light through a single slit can be visualized in terms of rays 3 and 4. An element at one edge of the slit and one just past the centerline are chosen, and the condition for minimum light intensity is that light from these two elements arrive 180° out of phase, or a half wavelength different in pathlength
First order minima:
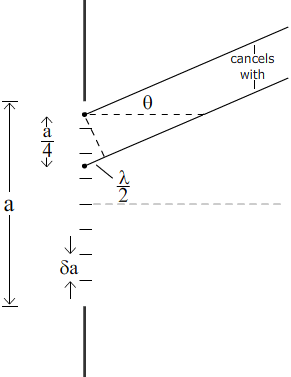
This animated sketch shows the angle of the first order minima: the first minimum on either side of the central maximum. We call the slit width a, and we imagine it divided into two equal halves. Using the Huygens’ construction, we consider a point at the very top of the slit, and another point a distance a/2 below it, i.e. a point at the very top of the lower half of the slit. Consider parallel rays from both points, at angle θ to the axis of symmetry.
The ray from the distance a/2 below has to travel an extra distance (a sin θ/2). If this distance is half a wavelength, i.e. if
asin θ= λ
then they are π/2 out of phase and they interfere destructively. Now, for every point in the top half of the slit, there is one in the bottom half a distance a/2 below and, at the angle that satisfies a sin θ = λ, they all interfere destructively.
So the first mimimum has sin θ = λ/a. On the other side of the axis of symmetry, sin θ = –λ/a is also a minimum. These two minima limit the broad central maximum.
Higher order minima:
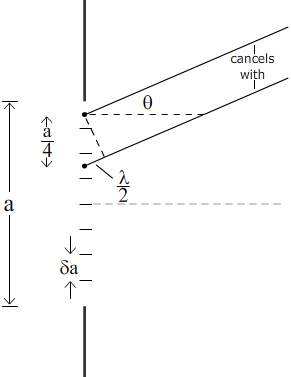
We divide the slit into any even number of equal slices. The diagram shows a division into four. Each half is divided into quarters, and light from a source in the first quarter cancels that from one in the second quarter. Similarly, sources in the third quarter are nullified by those in the fourth quarter. So this diagram represents the second order minima, where sin θ = λ/(a/2), or sin θ = 2λ/a. For the nth order minima, we have
asin θ= nλ, where n is an integer, but not zero.
Remember that, on the axis where θ = 0, there is a minimum, so the minima are equally spaced in sin θ, except either side of the central maximum.
We can note too that, for light diffracting the throught slits, the slit is usually much wider than a wavelength, so the pattern is usually very small, so the approximation that sin θ = θ is usually good.
Next we calculate how the intensity varies with sin θ.
Intensity I(θ):
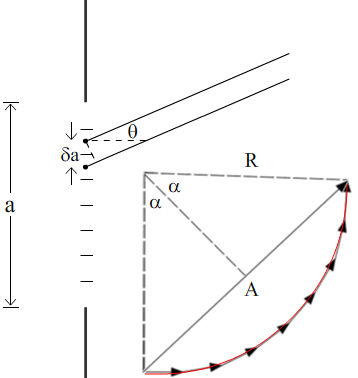
The slit of width a is divided into N slits, each of width δa. The path difference between rays from successive slices of the slit are equal, and so too are the angles between successive phasors. The slices of the slit all have equal width and length, so the lengths of all the phasors are equal. For a large number of slices, the phasors approximate the arc of a circle, as shown in red. We’ll call the angle that this subtends 2α. Now 2α is also the phase difference between the first and the last phasor, which is 2πa sin θ/λ.
α = πasin θ/λ.
The phasor sum has magnitude A, which we can write as R.sin α, where R is the radius of the arc formed by the phasor sum. On the axis, where the phasors are all in phase, the phasor sum is the straight line shown in red at right. This is the amplitude of the diffraction patter at θ /= 0, which we call A0. By the definition of angle, 2α = A0/R, which gives us R = A0/2α. So the magnitude of the phasor sum is
A= 2R.sin α = A0sin α/α.
As we’ve seen in several previous chapters, the intensity I is proportional to square of the amplitude A. So, using I0 for the intensity at the centre of the pattern, we have
I= I0(sin α/α)2 where α= πasin θ/λ.
