State and prove the perpendicular axis theorem Notes pdf ppt

Perpendicular Axis Theorem:

The theorem states that “the moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the lamina about any two mutually perpendicular axes in its plane and intersecting each other at the point where the perpendicular axis passes though it.”

 

This is applicable only to a plane lamina. The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the lamina about any two mutually perpendicular axes, passing in its own plane, intersecting each other at the point through which the perpendicular axis passes.

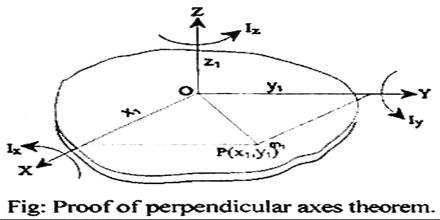
Explanation:

Let OZ be the axis perpendicular to the plane lamina and passing through point O. Let OX and OY be two mutually perpendicular axes in the plane of the lamina and intersecting at point O. If Ix, ly and lz are the moments of inertia of the plane lamina about the axes OX, OY and OZ respectively, then according to the theorem of perpendicular axes, Iz = Ix + ly

Proof:

 

Let, the lamina consists of n number of particles of masses m₁, m₂, m₃, . m_n.

and their positions are at the distances r₁, r₂, ……r_n respectively from the origin O.
For simplicity,

let a particle of mass m₁, is at point P (x₁, y₁) and its position is denoted by r₁.

So, r₁²  =  x₁² +y₁²

The moment of inertia of the particle of mass m, about OZ axis is,

I₁ = m₁r₁² = m₁ (x₁² + y₁²)

Similarly the of inertia of the particle of mass m₂ about OZ axes is, I₂ = m₂ (x₂² + y₂²) Therefore, the moment of inertia of the whole lamina about OZ axis is,

Iz = I₁ + I₂ + ……..       + I_n

= m₁ (x₁² + y₁²) + m₂ (x₂² + y₂²) + …….. + m_n (x_n² + y_n²)

= (m₁x₁² +m₂x₂² +…..+ m_nx_n²) + (m₁y₁² +m₂y₂²  +…..+ m_ny_n²)

So, Iz = Ix + ly [Proved]

Feedback is important to us.