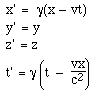The Lorentz Transform Equations for Physics:
After the review of Galilean transform equations lets look new transformation equations relating (x,y,z,t) and (x’,y’,z,t’). The motion is only in the x direction. They can again synchronize clocks: for convenience and symmetry, when they are side by side, they call that position zero and time zero. So x = 0 at t = 0 and x’ = 0 at t’ = 0. Further, at this moment, they can check that measurements in the y and z directions coincide, so two of the transformation equations are easy: y = y’ and z = z’. Same as Galileo.
However, we know that they disagree over time and length, so we need new transform equations for x and t. There is a good reason to try equations that are linear in x and t. First, we’ve seen that the time dilation and length contraction are linear in time and length. Second, if they are not linear, then we could end up have two solutions of x and t for a single event. This would be awkward for a frame that’s travelling with constant speed v! So let’s write:
x’ = Ax + Bt,
y’ = y,
z’ = z,
t’ = Ct + Dx.
where A, B, C and D are constants (ie independent of t and x: they will of course be functions of v, because at v = 0, we can see that A and C = 1, while B and D = 0. Now x’ = 0 marks the back of the train, so x = vt. Substituting in the first equation gives
A = −B/v.
At t = 0, Priya sees Ravi’s length contraction, so
x’ = γx = Ax
and by combining these equations we get:
x’ = γ(x – vt).
Now let’s look at time dilation, again from Priya’s point of view. At x = 0, he sees Ravi’s clock running slow, so t’ = γt, which gives
C = γ.
Now let’s look from the point of view of the back of the train, where x’ = 0. From this position, Ravi sees Priya’s clock running slow, so at x’ = 0, we have t = γt’. We also know that the train is moving at v with respect to Priya, so for the position x’ = 0, we also have x = vt. Substituting these into the last transformation equation gives
t/γ = γt – Dvt, whence
1 = γ2 – Dγv and so
D = (γ2 – 1)/γv.
This gives us the Lorentz transformation equations:
We should, of course, check that we get the correct length contraction and time dilation. This can be done by considering the particular cases of t = 0 and x = 0. And of course we should check that, in the limit where v is very much less than c, that these equations reduce to the Galilean transform above. If we set γ approximately equal to one, and v/c very much less than one, these equations do indeed reduce to the ones we use for Galilean relativity.