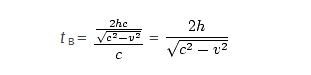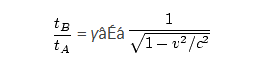Time Dilation Explained for Engineering Physics:
The most important and famous results in Special Relativity are that of time dilation and length contraction. Here we will proceed by deriving time dilation and then deducing length contraction from it. It is important to note that we could do it the other way: that is, by beginning with length contraction.
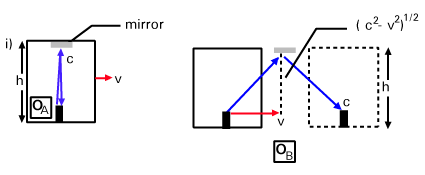
Consider the situations shown in the diagram. In i) we have the first observer OA at rest with respect to a moving train, which has velocity v to the right with respect to the ground. The carriage has a height h and has a mirror on the roof. OA designs a clock that measures the passage of time by firing a laser placed on the floor at the roof of the carriage and registering the time taken for it to hit the floor of the carriage again (after bouncing off the mirror on the roof). In OA ‘s frame the time taken for the laser light to reach is roof is just h/c and the roundtrip time is:
In the frame of an observer on the ground, call her O B , the train is moving with speed v (see ii) in ). The light then follows a diagonal path as shown, but still with speed c . Let us calculate the length of the upward path: we can construct a right-triangle of velocity vectors since we know the horizontal speed as v and the diagonal speed as c . Using the Pythagorean Theorem we can conclude that the vertical component of the velocity is ![]() as shown on the diagram. Thus the ratio the diagonal (hypotenuse) to the vertical is
as shown on the diagram. Thus the ratio the diagonal (hypotenuse) to the vertical is ![]() . But we know that the vertical of the right-triangle of lengths is h , so the hypotenuse, must have length
. But we know that the vertical of the right-triangle of lengths is h , so the hypotenuse, must have length ![]() . This is the length of the upward path. Thus the overall length of the path taken by the light in OB ‘s frame is
. This is the length of the upward path. Thus the overall length of the path taken by the light in OB ‘s frame is ![]() . It traverses this path at speed c , so the time taken is:
. It traverses this path at speed c , so the time taken is:
Clearly the times measured are different for the two observers. The ratio of the two times is defined as γ , which is a quantity that will become ubiquitous in Special Relativity.
Explanation:
All this might seem innocuous enough. So, you might say, take the laser away and what is the problem? But time dilation runs deeper than this. Imagine O A waves to O B every time the laser completes a cycle (up and down). Thus according to O A ‘s clock, he waves every t A seconds. But this is not what O B sees. He too must see O A waving just as the laser completes a cycle, however he has measured a longer time for the cycle, so he sees O A waving at him every t B seconds. The only possible explanation is that time runs slowly for O A ; all his actions will appear to O B to be in slow motion. Even if we take the laser away, this does not affect the physics of the situation, and the result must still hold. O A ‘s time appears dilated to O B . This will only be true if O A is stationary next to the laser (that is, with respect to the train); if he is not we run into problems with simultaneity and it would not be true that O B would see the waves coincide with the completion of a cycle.
What happens if we analyze the situation from O A ‘s point of view:
Unfortunately, the most confusing part is yet to come. What happens if we analyze the situation from O A ‘s point of view: he sees O B flying past at v in the backwards direction (say O B has a laser on the ground reflecting from a mirror suspended above the ground at height h ). The relativity principle tells us that the same reasoning must apply and thus that O A observes O B ‘s clock running slowly (note that γ does not depend on the sign of v ). How could this possibly be right? How can O A ‘s clock be running slower than O B ‘s, but O B ‘s be running slower than O A ‘s? This at least makes sense from the point of view of the relativity principle: we would expect from the equivalence of all frames that they should see each other in identical ways. The solution to this mini-paradox lies in the caveat we put on the above description; namely, that for t B = γt A to hold, O A must be at rest in her frame. Thus the opposite, t A = γt B , must only hold when O B is at rest in her frame. This means that t B = γt A holds when events occur in the same place in O A frame, and t A = γt B holds when events occur in the same place in O B ‘s frame. When v 0âá’γ 1 this can never be true in both frames at once, hence only one of the relations holds true. In the last example described (O B flying backward in O A ‘s frame), the events (laser fired, laser returns) do not occur at the same place in O A ‘s frame so the first relation we derived ( t B = γt A ) fails; t A = γt B is true, however.