What happens when two waves meet while they travel through the same medium? What effect will the meeting of the waves have upon the appearance of the medium? Will the two waves bounce off each other upon meeting (much like two billiard balls would) or will the two waves pass through each other? These questions involving the meeting of two or more waves along the same medium pertain to the topic of wave interference.
What is Interference?
Wave interference is the phenomenon that occurs when two waves meet while traveling along the same medium. The interference of waves causes the medium to take on a shape that results from the net effect of the two individual waves upon the particles of the medium. To begin our exploration of wave interference, consider two pulses of the same amplitude traveling in different directions along the same medium. Let’s suppose that each displaced upward 1 unit at its crest and has the shape of a sine wave. As the sine pulses move towards each other, there will eventually be a moment in time when they are completely overlapped. At that moment, the resulting shape of the medium would be an upward displaced sine pulse with an amplitude of 2 units.

Types of Interference:
- Constructive Interference
- Destructive Interference
Constructive Interference:
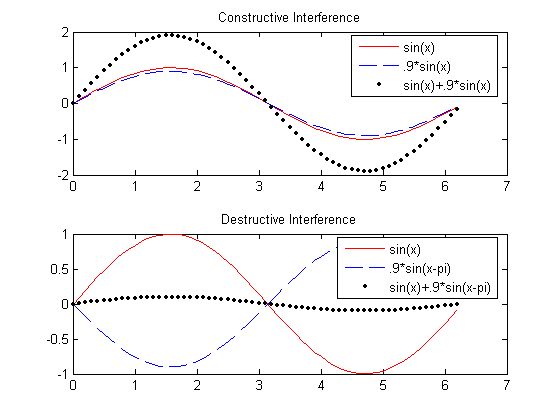
Constructive interference is a type of interference that occurs at any location along the medium where the two interfering waves have a displacement in the same direction. In this case, both waves have an upward displacement; consequently, the medium has an upward displacement that is greater than the displacement of the two interfering pulses. Constructive interference is observed at any location where the two interfering waves are displaced upward. But it is also observed when both interfering waves are displaced downward.
Destructive Interference:
Destructive interference is a type of interference that occurs at any location along the medium where the two interfering waves have a displacement in the opposite direction. For instance, when a sine pulse with a maximum displacement of +1 unit meets a sine pulse with a maximum displacement of -1 unit, destructive interference occurs.
Principle of superposition:
The task of determining the shape of the resultant demands that the principle of superposition is applied. The principle of superposition is sometimes stated as follows:
|
In the cases above, the summing the individual displacements for locations of complete overlap was made out to be an easy task – as easy as simple arithmetic:
| Displacement of Pulse 1 | Displacement of Pulse 2 | = | Resulting Displacement |
| +1 | +1 | = | +2 |
| -1 | -1 | = | -2 |
| +1 | -1 | = | 0 |
| +1 | -2 | = | -1 |
In actuality, the task of determining the complete shape of the entire medium during interference demands that the principle of superposition be applied for every point (or nearly every point) along the medium.
