Concept of Newton’s Rings for Engineering Physics B.Tech 1st Year

What is Newton’s Ring?

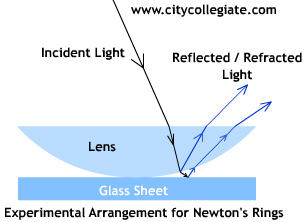
When a plano-convex lens with its convex surface is placed on a plane glass sheet, an air film of gradually increasing thickness outward is formed between the lens and the sheet. The thickness of film at the point of contact is zero. If monochromatic light is allowed to fall normally on the lens, and the film is viewed in reflected light, alternate bright and dark concentric rings are seen around the point of contact. These rings were first discovered by Newton, that’s why they are called NEWTON’S RINGS.

WHY NEWTON’S RINGS ARE FORMED?

The occurrence of the Newton’s rings can be explained on the basis of Wave theory of light

1. An air film of varying thickness is formed between the lens and the glass of sheet
2. When a light ray is incident on the upper surface of the lens, it is reflected as well as refracted
3. When the refracted ray strikes the glass sheet, it undergoes a phase change of 180 degree on reflection
4. Interference occurs between the 2 waves, which interfere constructively if path difference between them is (m+1/2) ? (where m is the ring number) and interferes destructively, if path difference between them is m ?  producing alternate bright and dark rings.

The radius of the rings:

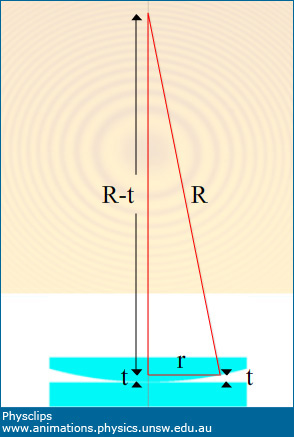
Let’s consider a dark ring with radius r at a point where the separation is t. The right angled triangle shown in red has a height R–t so Pythagoras’ theorem gives us

R²  =  (R − t)² + r²      which gives
R²  = R² − 2Rt + t² + r²       and so
2Rt  = t² + r²

Here, t is several wavelengths or so, while the ring radius r is usually some millimeters, so we can neglect the t² term. Further, for a dark ring, we have seen above that t = mλ/2, where m is a positive integer. Substituting gives

Rmλ=r^{2     or}        r= (Rmλ)½

So a plot of r² vs m, the number of the dark ring, gives a straight line whose slope is Rmλ.

Feedback is important to us.