Phase Rule And Its Application To One Component System (Water And Sulphur)

INTRODUCTION OF PHASE RULE:

The phase rule is a generalization given by Willard Gibbs (1874), which seeks to explain the equilibria existing in heterogeneous system. It may be stated as: “provided the equilibrium between any number of phases is not influenced by gravity, or electrical, or magnetic forces or by surface action and only by temperature, pressure and concentration, then the number of degrees of freedom (F) of the system is related to number of components (C) and of phases (P) by the phase rule equation for any system at equilibrium at a definite temperature and pressure.

                                                     F = C – P + 2

This rule, if properly applied, has no exception.

Explanation of terms:

Phase:

A phase is defined as “an homogeneous, physically distinct and mechanically separable portion of system, which is separated from other such parts of the system by definite boundary surface”. For Example:

• At freezing point, water consists of three phase :

Ice _(s) Water _(l) Water vapour _(g)

• A gaseous mixture, being thoroughly miscible in all proportion, will constitute one phase only. Thus, a mixture of N₂ and H₂ forms phase only.
• If two liquids are immiscible (i.e., benzene and water), they will form two separate phase only.
• If two liquids are miscible (i.e., alcohol and water), they will form one liquid phase only.
• A solution of a substance in a solvent consists of phase only, e. g, glucose solution in water.
• Each solid mark up a separate phase, except in the case of solid solution, e. g, many forms of sulphur can exist together, but these are all separate phases.
• A heterogeneous mixture like :

CaCO3 _(s)   CaO_(s) + CO_{2 (g)}

Consists of three phases   (i.e., two solids and one gasous). Similarly, in the equilibrium reaction,

Fe_(s)  +  H₂O  FeO_(s) + H_2(g)

There are two solid phases, Fe and FeO and one gaseous phase consisting of H₂O_(g) and H_2(g). Thus, three phases exists in equilibrium.

• A homogeneous solid solution of a salt constitutes a single phase. Thus, Mohr’s [ FeSO₄ (NH₄)₂SO₄6H₂O] solution constitutes a single phase, although it consists of FeSO₄ (NH₄) SO₄, and  H₂O.

Component:

by the term component is meant “the smallest number of independent variable constituents, taking part in state of equilibrium, by mean of which the composition of each phase can be expressed in the form of chemical equation”. For example:

i.            In the water system,

Ice _(s) Water _(l) vapour _(g)

The chemical composition of all the three phases is H₂O. Hence, it is one component system.

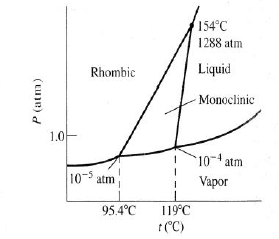
ii.            the sulphur system consists of four phases, rhombic, monoclinic, liquid and vapour, the chemical composition of all phases is S. hence, it is one component system.

iii.            In the dissociation of NH₄CI in a closed vessel,

NH₄CI_(g)NH₄CI_(g) NH_3(g)+HCI_(g)

The proportions of NH₃ and HCl are equivalent and hence, the composition of both phases (solid and gaseous) can be expressed in terms of NH₄CI alone. Hence, the number of component is one. However, if NH₃ or HCl  is in excess, the system become a two component system .

iv.            A system of saturated solution of NaCI consists of solid salt, salt solution and water vapour. The chemical composition of all the three phases can be expressed in terms of NaCI and  H₂O. Hence, it is a two component system.

 

v.            In the thermal decomposition of CaCO₃

CaCO_3(s)      CaO_(s) + CO_2(g)

The composition of each of the three phases can be expressed in terms of at least any two of the independently variable constituents, CaCO₃, Cao and  CO₂. Suppose  CaCO₃ and CaO are chosen as the two components, the composition of different phases is represented as follows:

Phase: CaCO₃ = CaCO₃ + 0 CaO

Phase: CaO = 0 CaCO₃ + CaO

Phase: CO₂ = CaCO₃ – CaO

Thus, it is two component systems.

vi.            In the dissociation reaction,

CuSO₄5H₂O_(s)    CuSO_4.3H₂O_(s) +2H₂O_(g)

The composition of each phase can be represented by the simplest component, CuSO₄ and H₂O

Hence, it is two component systems.

vii.            In the equilibrium, Fe_(s) + H₂O_(g) FeO_(s) + H_2(g), the minimum components required the composition phase is three. Evidently, it is a three component system.

Number of component of a system may alternatively be defined as the number of chemical constituents of the system minus the number of equations relating to these constituents in an equilibrium state. For example:

1.Dissociation of KClO₃ in a closed vessel: following equilibrium exists :KClO_3(s) 2KCl_(s) + 3O_{2 (g)}

No. of constituents = 3

Now  

No. of equations relating the concentration of constituents =1.

Hence, number of components = 3-1 = 2 i.e., it is a two component system.

2. Dissociation of NH₄Cl:

i.            Only   NH₄Cl is heated in a closed vessel. The equilibrium   existing is:   NH₄Cl_(s)  NH_3(g) +HCl_(g)

[NH₃]  =  [HCl]

Also               K_eq  = = [NH₃][HCl]

Because the active mass of NH₄Cl_(s) is constant.

Now number of components, C

= No. of constituent –[ No, of equations relating to concentration of constituents]

=  3(NH₄CL, NH₃ and HCl) – 2 = I, i.e. it is a single component system :

ii.            When NH4Cl is heated in a closed vessel along with NH3 or HCl, At equilibrium:

Keq  =  [NH3][HCl]    ……………..(i)

But              [NH3]    ≠   [HCl] …………(ii)

Only one equation (i) relates the concentrations of constituents

No. of component, (C) = 3 -1 = 2, i.e. under the above conditions, the system has two components.

Merits of phases rule:

1.  It is applicable to both physical and chemical equilibria.

2. It require no information regarding molecular/ micro-structure, since it is applicable to

macroscopic system.

3. It is a convenient method of classifying equilibrium states in terms of phases, components

and degrees of freedom.

4. It helps us to predict the behaviour of a system, under different sets of variables.

5. It indicates that different systems with same degree of freedom behave similarly.

6. It does not take into cognizance of either the nature or quantities of component present in

the system.

7. It helps in deciding whether under a given set of condition:

a. various substances would exist together in equilibrium or

b. some of the substances present would be interconverted or

c. some of the substances present would be eliminated .

Limitation of phase rule:

1. It can be applied only for system in equilibrium. Consequently, consequently, it is of little value in case of very slow equilibrium state attaining system.

2. It applies only to a single equilibrium system: and provided no information regarding any other possible equilibria in the system.

3. It requires utmost care in deciding the number of phases existing in an equilibrium sate, since it considers only the number of phases, rather than their amounts. Thus, even if a trace of the phase is present, it accounts towards the total number of phases.

4. It conditions that all phases of the system must be present simultaneously, under the identical conditions of temperature and pressure.

5. It conditions that solid and liquid phases must not be in finely –divided state; otherwise deviations occurs.

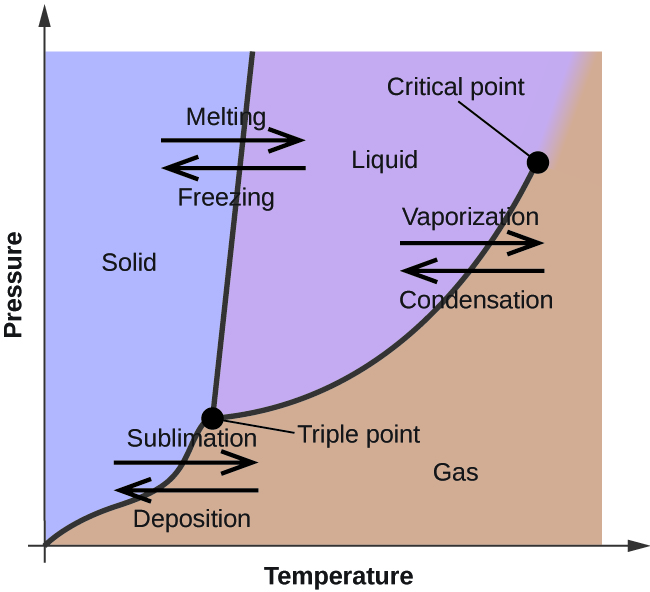
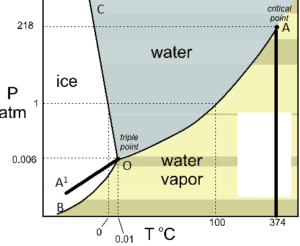
WATER SYSTEM

The water system consists of three phases , viz., ice, water and water vapour.

Ice_(s)        Water _(I)       Water vapour _(g)

 

 

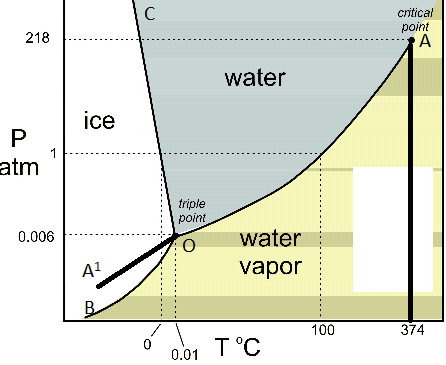
Since H₂O is the only chemical compound involved, therefore, it is single or one-component system . From the phase rule, when C =1,

F = C – P + 2 =1 – P + 2 = 3 – P

i.e, the degree of freedom depends on the number of phases present at equilibrium. Three different case are possible :

(i) P = 1 ;      F = 2                                           (bivariant system)

(ii) P = 2 ;      F = 1                                           (univariant system)

(iii) P = 3 ;     F = 0                                          (invariant system)

From the above , it is clear that for any one-component system , the maximum number of degrees of freedom is two. Therefore, such a system can be represented completely by a two-dimensional

Diagram. The most convenient variable are the pressure and the temperature. The water system is shown in Fig. 1 The diagram consists of :

1. Areas :  AOB. AOC and BOC are the fields of existence of vapour, liquid and ice phase respectively Within these single-phase areas, the system in bivariant , because to locate any point in an area, temperature as well as pressure co-ordinates need to be know.. This also following from phase rule equation : F = 3 – P = 3 – 1 = 2 .

2. Boundary lines: separating the areas are lines OA, OB and OC, connecting the point at which two phases can co-exist in equilibrium. In order to locate any point on a particular line, either temperature or pressure co-ordinate should be known, because for fixed value of one co-ordinate, the second is automatically fixed, In other words, any point on boundary lines has one degree of freedom or is univariant. This also follows from phase rule equation : F = 3 – P = 3 – 2 = 1.

The curve OA, dividing the liquid from the vapour region, is called vapour pressure curve of liquid water or vaporization curve. At any given temperature, there is one and only one pressure at which water vapour is in equilibrium with liquid water. Similarly , at any given pressure, there is one temperature at which water vapour is in equilibrium with liquid water. In other words, the system is univariant. i.e,, has one degree of freedom. The curve OA has a natural upper limit at +374 C. which is the critical-point, beyond which the phase merges into vapour phase and they are no longer distinguishable from each other.

The curve OB is the sublimation curve of ice. It gives the conditions under which water vapour is in equilibrium with solid ice. The point B has a natural limit at -273^oC, beyond which the two phases merge into each other.

The curve OC ,  which divies the solid –ice region from the liquid – water region, is called melting curve, because it indicates how the melting temperature of ice or the freezing tempereature of water  varies with the pressure. The slope of OC towards the pressure axis shows that the melting point of ice is decreased by increasing pressure.

3. Triple point:     The three curves OA, OB, and OC meet at O, at which solid, liquid and vapour are simultaneously at equilibrium. This point at 273.16 k is called a triple – point. Since three phases co-exist, the system is invariant (F=3-3=0). In other words, there is no degree of freedom at O, i.e., neither pressure nor temperature can be altered, even slightly, without causing the disappearance of one of the phase.

4.Metastable curve OA’: As water does not always freeze at 0oC, so if the vessel containing water and vapour is perfectly clean and free from dust, it is possible to super – cool water several degrees below its freezing point 0. The dotted curve OA’, a continuation of vaporization curve AO, represents the pressure curve of super cooled water. This curve represents a metastable system. On slight disturbance, the super cooled water at once changes to solid ice. It may be noted that metastable vapour pressure of supper cooledh water is higher than the vapour pressure of ice.

Feedback is important to us.