Resolution of Vectors:
Resolution of vectors is the opposite action of addition of vectors. For a given vector A, we may find a pair of vectors A-; and A; in any two given direction. Refer Fig. 2.5(a).
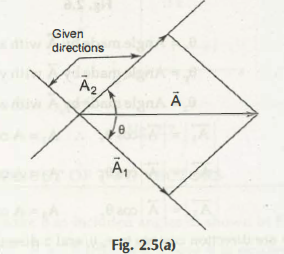
Fig. 2.5(b) shows that vector A is replaced by its components A1 and A2 and A is no longer operative.
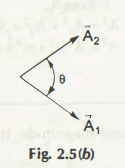
Here, A1 and A2 are called the component vectors. The stipulated directions may include any angle e. If e = 90°, the components are called rectangular components.
We can also resolute A in space into three orthogonal components which are not in the same plane.
We first resolve A into two components A3 and A4 as shown in Fig. 2.6. Then A4 can be resolved into A1 and A2 which are in x and y directions respectively. Thus, finally A is resolved into three orthogonal components A1, A2, A3 in x, y and z directions.
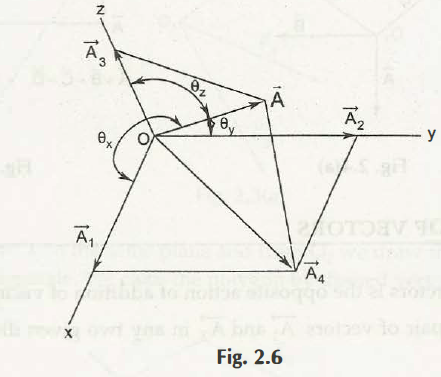
Let
θ = Angle made by A with x axis
θ = Angle made by A with y axis
θ = Angle made by A with z axis.
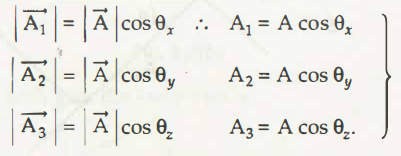
If l, m and n are direction cosines in x, y, and z directions respectively, we can write
L =cos θx A1=Al
M=cos θ y, A2 =Am
N =cos θ z, A3 =An
From (1.2) and (1.3) à A2 =A12 +A22+A32
A2 =A2 (L2+M2=N2 ) L2 +M2 +N2 =1
