Galilean Transform Equations Notes for Engineering Physics BTech 1st Year:
Galilean Transformation Definition, Galilean Transformation Explanation:
In An introduction to the mechanics of Galileo and Newton, we saw that converting between two inertial frames was easy. Let’s consider motion in the x direction, with relative speed v: the train goes past the station at v (on a straight and level track that we call the x axis). We synchronise watches (set t = 0) at some convenient time, let’s say when the back of the train passes Priya, the observer in the station.
So the position of the back of the train is x = vt, where t is the time elapsed. If Ravi, a passenger in the train, is a distance x’ ahead of the back of the train, then Priya sees her position as x = vt + x’, where we use the prime (‘) to signify Ravi’s frame and the absence of it to signify Priya’s.
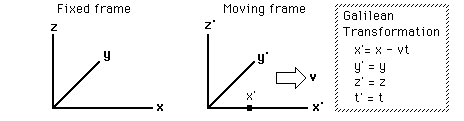
Formally, we should consider the y and z directions too. In Galilean relativity, there is no reason for Priya and Ravi to disagree on how far she is above the floor (so z = z’) or how far sideways she is from the aisle (so y = y’). Further, we’ve made the assumption (for Galilean relativity) that their measurements of time are the same, so Ravi’s time t’ = t. So the transform equations for Galilean relativity (motion v in the x direction) are:
x = vt + x’,
y = y’,
z = z’, and
t = t’.
We’ve already seen that, if Ravi walks at speed u’ and acceleration a’, Priya sees her speed u with respect to him as:
u = v + u’, and
a = a’
for motion in the x direction. Now we can see that this follows from the equations above by differentiation.
For relativity, we need new transform equations because, as we have seen, when v becomes comparable with the speed of light. Ravi and Priya disagree on time and length.