Area Moment of Inertia:
The second moment of the area around a given axis is called the area moment of inertia
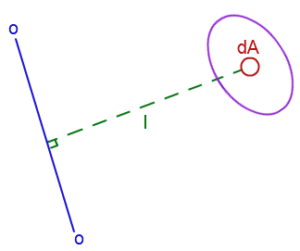
Now, for the above figure we have the axis 0 given and hence we can calculate the moment of area by summing together l2 dA for all the given elements of area dA in the yellow region.
Hence Area moment of inertia,
![]()
For a rectangular region the area moment of inertia

Units to express it : Imperial units: inches4
Metric units: mm4, cm4, m4
Mass Moment of Inertia:
The mass moment of inertia is the measurement of the distribution of the mass of an object or body relative to a given axis. It is represented by the symbol I.
The formula for a single particle of mass m is
![]()
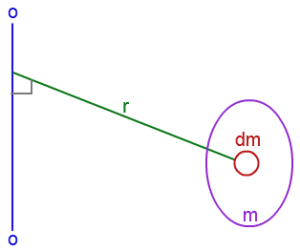
Units : kg/m2
Mass moment for rigid bodies: Here the body is thought of as sum of particles each having mass dm.
The formula is,
![]()
Similarly,
![]()
where,
p = density
If calculated over area then
![]()
Moment of Inertia Circle:
For circle the area moment of inertia through centroid is as follows

The moment of inertia is calculated as
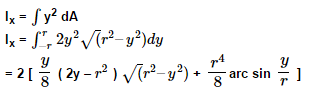
Solving this we get,
![]()
Similarly, we find for Iy, where
![]()
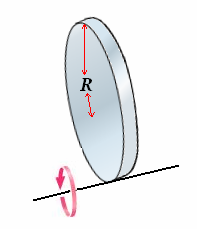
Moment of Inertia of a Disk:
- For a solid disk having the axis of rotation as center the moment of inertia is given by
![]()
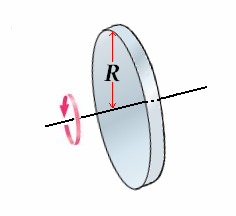
- For a solid disk having the axis of rotation as rim moment of inertia is given by
![]()
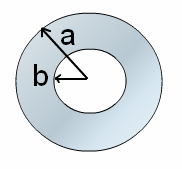
- For a disk with the hole on the axis of rotation as center, moment of Inertia is given by,
![]()
Moment of Inertia Rectangle:
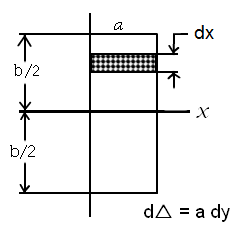
For rectangle the calculations are done as follows
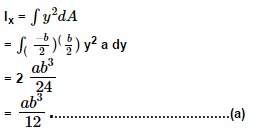
Moment of Inertia Cylinder:
The Moments of Inertia of cylinder with different axis are given below:
Solid cylinder with axis of rotation as centre = ![]()
Solid cylinder with axis of rotation as surface = ![]()
Hallow cylinder with axis of rotation as centre = ![]()
Hallow cylinder with axis of rotation as surface = 2 MR2
Moment of Inertia Sphere:
The moment of inertia of a solid sphere with axis of rotation as center is
![]()
The moment of inertia of a solid sphere with axis of rotation as surface is
![]()
