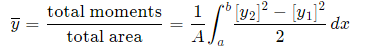Centroid for Curved Areas: Notes pdf ppt Engineering Mechanics

Centroid for Curved Areas:

Taking the simple case first, we aim to find the centroid for the area defined by a function f(x), and the vertical lines x = a and x = b as indicated in the following figure.

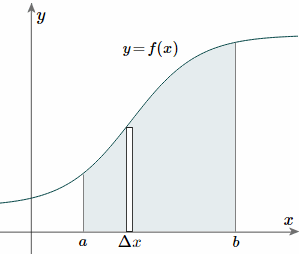
To find the centroid, we use the same basic idea that we were using for the straight-sided case above. The “typical” rectangle indicated is $x$ units from the $y$-axis, and it has width $\mathrm{\Delta }x$ (which becomes $dx$ when we integrate) and height y = f(x).

Generalizing from the above rectangular areas case, we multiply these 3 values ($x$, $f\left(x\right)$ and $\mathrm{\Delta }x$, which will give us the area of each thin rectangle times its distance from the $x$-axis), then add them. If we do this for infinitesimally small strips, we get the $x$-coordinates of the centroid using the total moments in the x-direction, given by:

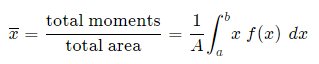
And, considering the moments in the y-direction about the x-axis and re-expressing the function in terms of y, we have:

 

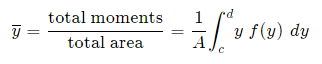
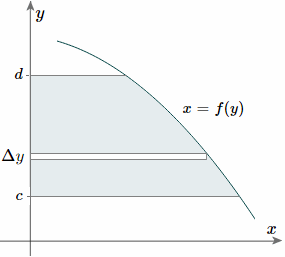
Notice this time the integration is with respect to $y$, and the distance of the “typical” rectangle from the $x$-axis is $y$units. Also note the lower and upper limits of the integral are $c$ and  $d$, which are on the  $y$-axis.

Of course, there may be rectangular portions we need to consider separately. (I’ve used a different curve for the ​y ​​​case for simplification.)

Alternate method:

Depending on the function, it may be easier to use the following alternative formula for the y-coordinate, which is derived from considering moments in the x-direction (Note the “dx” in the integral, and the upper and lower limits are along the x-axis for this alternate method).

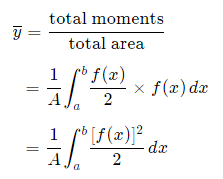
This is true since for our thin strip (width $dx$), the centroid will be half the distance from the top to the bottom of the strip.

Another advantage of this second formula is there is no need to re-express the function in terms of y.

Centroids for Areas Bounded by 2 Curves:

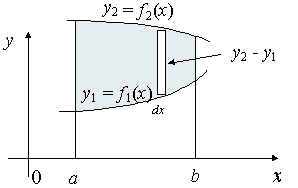
We extend the simple case given above. The “typical” rectangle indicated has width Δx and height y₂ − y₁, so the total moments in the x-direction over the total area is given by:

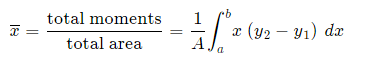
For the y coordinate, we have 2 different ways we can go about it.

 

Method 1: We take moments about the y-axis and so we’ll need to re-express the expressions x₂ and x₁ as functions of y.

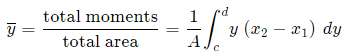
Method 2: We can also keep everything in terms of x by extending the “Alternate Method” given above:

Feedback is important to us.