If two or more forces are acting simultaneously at apoint, the same effect can be produced by a single forceof the proper size and direction. This single force,which is equivalent to the action of two or more forces,is called the resultant. Putting component forcestogether to find the resultant force is called compositionof forces. (See fig. 2-2.) The vectors representing theforces must be added to find the resultant. Because avector represents both magnitude and direction, themethod for adding vectors differs from the procedureused for scalar quantities (quantities having onlymagnitude and no direction). To find the resultant force when a force of 5 pounds and a force of 10 pounds are applied at a right angle to point A, refer to figure
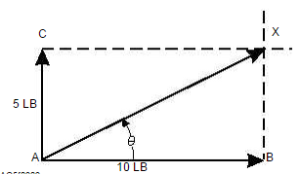
2.The resultant force may be found as follows:Represent the given forces by vectors AB and ACdrawn to a suitable scale. At points B and C drawdashed lines perpendicular to AB and AC, respectively.From point A, draw a line to the point of intersection X,of the dashed lines. Vector AX represents the resultantofthetwoforces.Thus,whentwomutuallyperpendicular forces act on a point, the vectorrepresenting the resultant force is the diagonal of arectangle. The length of AX, if measured on the samescale as that for the two original forces, is the resultantforce; in this case approximately 11.2 pounds. Theangle gives the direction of the resultant force withrespect to the horizontal.Mathematically,theresultantforceofperpendicular forces can be found by using thePythagorean theorem which deals with the solution ofright triangles. The formula is C2 = a2 + b2. This statesthat the hypotenuse, side “C” (our unknown resultantforce) squared is equal to the sum of side “a” (one of ourknown forces) squared and side “b” (another of ourknown forces) squared.
