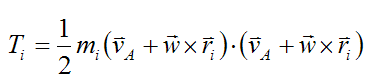Derivation of the Kinetic Energy Equations for a Rigid Body Notes pdf ppt

Kinetic Energy For A Particle:

The kinetic energy for a particle is given by the following scalar equation:

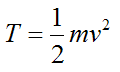……..(1)

Where:

T is the kinetic energy of the particle with respect to ground (an inertial reference frame)

m is the mass of the particle

v is the velocity of the particle, with respect to ground

Kinetic Energy For A Rigid Body:

Planar Motion

For a rigid body experiencing planar (two-dimensional) motion, the kinetic energy is given by the following general scalar equation:

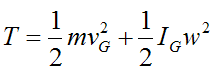……….(2)

Where:

T is the kinetic energy of the rigid body with respect to ground

m is the mass of the rigid body

v_G is the velocity of the center of mass G of the rigid body, with respect to ground

I_G is the moment of inertia of the rigid body about an axis passing through the center of mass G, and perpendicular to the plane of motion

w is the angular velocity of the rigid body, with respect to ground

Three Dimensional Motion:

For general three-dimensional motion, the kinetic energy of a rigid body is given by the following general scalar equation:

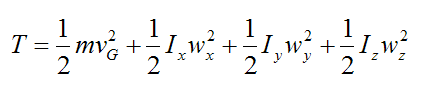…….(3)

Where:

T is the kinetic energy of the rigid body with respect to ground

m is the mass of the rigid body

v_G is the velocity of the center of mass G of the rigid body, with respect to ground

w_x, w_y, w_z are the components of the angular velocity of the rigid body with respect to ground, and resolved along the local xyz axes (see figure below). To calculate these components, one must first determine the angular velocity vector of the rigid body with respect to the global XYZ axes, and then resolve this vector along the x, y, z directions to find the components w_x, w_y, w_z. This is often done using trigonometry.

Derivation of the kinetic energy equations for a rigid body:

The equations for planar (two-dimensional) motion follow naturally from the equations for general three-dimensional motion, so it is only necessary to derive the kinetic energy equations for three-dimensional motion.

To derive the previous expressions for the kinetic energy of a rigid body we must apply the equation for kinetic energy of a small mass element in the rigid body, and then sum it over the entire rigid body. This problem is set up as shown in the figure below.

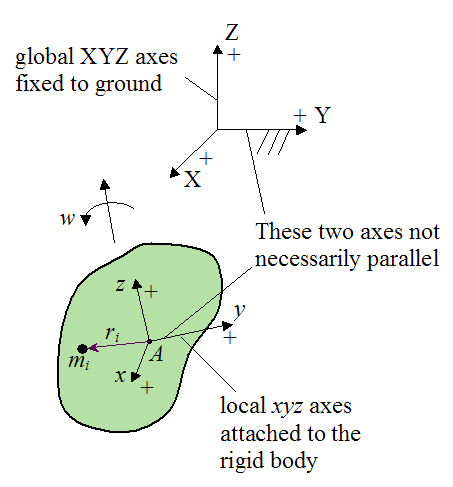
For a small mass element m_i in the rigid body the kinetic energy is given by the following scalar equation:

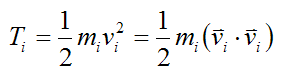………..(4)

Where:

T_i is the kinetic energy of the small mass element, with respect to ground

m_i is the mass of the small mass element in the rigid body. This mass element is small enough to be considered a particle

v_i is the velocity vector of this small mass element with respect to ground, and resolved along the local xyz axes. To calculate this velocity, one must first determine the velocity vector v_i with respect to the global XYZ axes, and then resolve this vector along the local xyz axes. This is often done using trigonometry.

Now, from the equations for general motion of a rigid body:

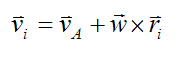…………………(5)

Where:

v_A is the velocity of point A with respect to ground, and resolved along the local xyz axes. To calculate v_A, one must first determine v_A with respect to the global XYZ axes, and then resolve this vector along the local xyz axes. This is often done using trigonometry.

w is the angular velocity of the rigid body with respect to ground, and resolved along the local xyz axes. To calculate w, one must first determine w with respect to the global XYZ axes, and then resolve this vector along the local xyz axes. This is often done using trigonometry.

r_i is the position vector from point A to the location of m_i. This vector is measured relative to the local xyz axes.

Substituting equation (4) into equation (5) we get

 

Feedback is important to us.