Resultant of Parallel Coplanar Forces:
The forces, which are having their line of action parallel to each other, are known parallel forces. The two parallel forces will not intersect at a point.
The following are the important types of parallel forces :
1. Like parallel forces,
2. Unlike parallel forces.
1. Like parallel forces. The parallel forces which are acting in the same direction, are known as like parallel forc.es. In Fig. 1.58, two parallel forces F1 and F2 are shown. They are acting in the same direction. Hence they are called as like parallel forces. These forces may be equal or unequal in magnitude.
Unlike Parallel Forces:
The parallel forces which are acting in the opposite direction, are known as unlike parallel forces. In Fig. 1.59, two parallel forces F1 F2 are acting in opposite direction. Hence they are called as unlike parallel forces. These forces may be equal or unequal in magnitude.
The unlike parallel forces may be divided into : (i) unlike equal parallel forces, and (ii) unlike unequal parallel forces.
Unlike equal parallel forces are those which are acting in opposite direction and are equal in magnitude.
Unlike unequal parallel forces are those which are acting in opposite direction and are unequal in magnitude.
The resultant of following two parallel forces will be considered:
1. Two parallel forces are like.
2. Two parallel forces are unlike and are unequal in magnitude.
3. Two parallel forces are unlike but equal in magnitude.
Resultant of Two Like Parallel Forces:
Fig. 1.60 shows a body on which two like parallel forcesF1 andF2 are acting. It is required to determine the resultant (R) and also the point at which the resultant R is acting. For the two parallel forces which are acting in the same direction, obviously the resultant R is given by,
R =F1 +F2
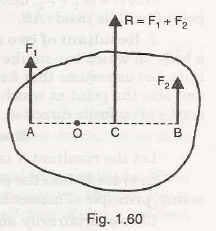
In order to find the point at which the resultant is acting, F Varignon’s principle (or method of moments) is used. According 1 60 IQ to this, the algebraic sum of moments of F 1 and F2 about any point should be equal to the moment of the resultant (R) about that point. Now arbitrarily choose any point 0 along line AB and take moments of all forces about this point.
Moment of F 1 about 0 = F 1 x AO (clockwise)(-)
Moment of F2 about 0 = F2 x BO (anti-clockwise)(+ ve)
. . Algebraic sum of moments of F1 and F2 about O= – F 1 x AO + F 2 x BO
Moment of resultant about 0 = Rx OC (anti-clockwise){+)
But according to principle of moments the algebraic sum of moments of F 1 and F2 about
0 should be equal to the moment of resultant about the same point 0.
F 1 x AO + F2 x BO = +R x CO= (F1 + F2) x CO
or . F1(AO +CO)= F2(BO- CO)
F l x AC = F 2 x BC
F1 / F2 = BC / AC
The above relation shows that the resultant R acts at the pointe, parallel to the lines of action of the given forcesF1 andF2 in such a way that the resultant divides the distance AB in the ratio inversely proportional to the magnitudes of F 1 and F2 Also the point C lies in line AE i.e., point C is not outside AB.
The location of the pointe, at which the resultant R is acting, can also be determined by taking moments about points A of Fig. 1.60. As the forceF1 is passing through A, the moment of F 1 about A will be zero.
The moment of F 2 about A= F2 x AB (anti-clockwise)(+)
Algebraic sum of moments of F 1 and F2 about 0
= 0 + F2 x AB = F2 x AB (anti-clockwise) (+)
The moment of resultant R about A
= R x AC (anti-clockwise)(+)
But according to the principle of moments, the algebraic sum of moments of F1 and F 2
about A should be equal to the moment of resultant about the same point A. Hence equating
equations (i) and (ii),
F2 x AB =R x AC
But R = (F 1 + F2 ) hence the distance AC should be less than AB. Or in other words, the
point C will lie inside AB.
Resultant of Two Unlike Parallel Forces (unequal in magnitude):
Fig 1.61 shows
a body on which two unlike parallel forces F 1 and F2 are acting which are unequal in magnitude. Let us assume that forceF1 is more than F2• It is required to determined the resultant and also the point at which the resultant R is acting. For the two parallel forces, which are acting in opposite direction, obviously the resultant is given by,
R=F1 -F2
Let the resultant R is acting at C as shown in Fig. 1.61.
In order to find the point C, at which the resultant is acting, principle of moments is used.
Choose arbitrarily any point 0 in line AB. Take the moments of all forces (i.e., Fp F2 and R) about this point.
Moment of F 1 about 0 = F 1 x AO (clockwise)
Moment of F2 about 0 = F2 x BO (clockwise)
Algebraic sum of moments of F 1 and F2 about 0
=F1 x AO +F2 x BO
Moment of resultant force R about 0
= R x CO (clockwise)
= (F1 – F2) x CO
= F1 x CO –F2 x CO
But according to the principle of moments, The algebraic sum of moments of all forces about any point should be equal to the moment of resultant about that point. Hence equating equations (i) and (ii), we get
F 1 x AO + F2 x BO = F 1 x CO – F 2 x co
F2(BO +CO) = F 1(CO -AO)
F2 x BC=F1 x AC
BC / AC = F1 / F2 or F1 / F2 = BC / AC
But F1 >F2, hence BC will be more than AC. Hence point O lies outside of AB and on the same side as the larger force F1 Thus in case of two unlike parallel forces the resultant lies de the line joining the points of action of the two forces and on the same side as the larger
The location of the Point C, at which the resultant R is acting, can also be determined by taking moment about point A, of F1g. 1.61. As the force F1 is passing through A, the moment of F1 about A will be zero.
The moment of F2 about A= F2 x AB (clockwise)(-)
Algebraic sum of moments of F 1 and F2 about A
= O + F2 x AB = F2 x AB (clockwise)(- ) … (i)
The moment of resultant R about A should be equal to the algebraic sum of moments of F1 and F2 (i.e.,= F2 x AB) according to the principle of moments. Also the moment of resultant R about A should be clockwise. As R is acting upwards [ ·: F1 > F2 and R = (F1 – F2) so R is acting in the direction ofF1], the moment of resultant R about A would be clockwise only if the points C is towards the left of point A. Hence the point C will be outside the line AE and on the side of F 1 (i.e. , larger force).
Now the moment of resultant R about A
= R x AC (clockwise)(-) … (ii)
Equating equations (i) and (ii),
F2 x AB =R x AC
= (F1 -F2) x AC (·: R=F1 – F2)
As F1, F2 and AB are known, hence AC can be calculated. Orin other words, the location of point C is known.
Resultant of Two Unlike Parallel Forces which are Equal in Magnitude:
When two equal and opposite parallel forces act on a body, at some distance apart, the two forces from a couple which has a tendency to rotate the body. The perpendicular distance between the parallel forces is known as arm of the couple.
Fig. 1.62 shows a body on which two parallel forces, which are acting in opposite direction but equal in magnitude are acting. These two forces will form a couple which will have a tendency to rotate the body in clockwise direction. The moment of the couple is the product of either one of the forces and perpendicular distance between the forces.
Let F =Force at A or at B
a= Perpendicular distance (or arm of the couple)
The moment (M) of the couple is given by, M = F x a.
The units of moment will be Nm.
