The Moment of a force is a measure of its tendency to cause a body to rotate about a specific point or axis. This is different from the tendency for a body to move, or translate, in the direction of the force. In order for a moment to develop, the force must act upon the body in such a manner that the body would begin to twist. This occurs every time a force is applied so that it does not pass through the centroid of the body. A moment is due to a force not having an equal and opposite force directly along it’s line of action.
Imagine two people pushing on a door at the doorknob from opposite sides. If both of them are pushing with an equal force then there is a state of equilibrium. If one of them would suddenly jump back from the door, the push of the other person would no longer have any opposition and the door would swing away. The person who was still pushing on the door created a moment.
Elements of a Moment
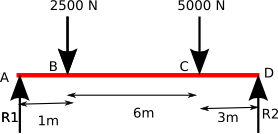
The magnitude of the moment of a force acting about a point or axis is directly proportional to the distance of the force from the point or axis. It is defined as the product of the force (F) and the moment arm (d). The moment arm or lever arm is the perpendicular distance between the line of action of the force and the center of moments.
Moment = Force x Distance or M = (F)(d)
The Center of Moments may be the actual point about which the force causes rotation. It may also be a reference point or axis about which the force may be considered as causing rotation. It does not matter as long as a specific point is always taken as the reference point. The latter case is much more common situation in structural design problems.
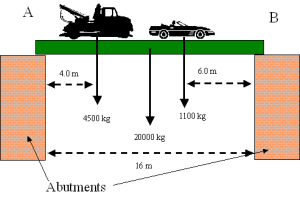
A moment is expressed in units of foot-pounds, kip-feet, newton-meters, or kilo newton-meters. A moment also has a sense; A clockwise rotation about the center of moments will be considered a positive moment; while a counter-clockwise rotation about the center of moments will be considered negative. The most common way to express a moment is
