Experimental evidence and theoretical models are presented supporting the conjecture that dry friction stick-slip is described by self-organized criticality. We use the data, obtained with a pin-on-disk tribometer set to measure lateral force, to examine the variation of the friction force as a function of time. We study nominally flat surfaces of matching aluminum and steel. The probability distribution of force drops follows a negative power law with exponent’s mu in the range 3.2-3.5. The frequency power spectrum follows a 1/f alpha pattern with alpha in the range 1-1.8.
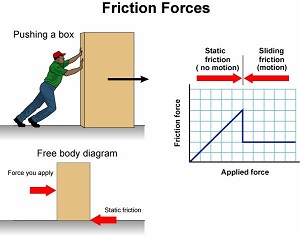
We first compare these experimental results with the well-known Robin Hood model of self-organized criticality. We find good agreement between theory and experiment for the force-drop distribution but not for the power spectrum. We explain this on a physical basis and propose a model which takes explicitly into account the stiffness and inertia of the tribometer. Specifically, we numerically solve the equation of motion of a block on a friction surface pulled by a spring and show that for certain spring constants the motion is characterized by the same power law spectrum as in experiments. We propose a physical picture relating the fluctuations of the force drops to the microscopic geometry of the surface.
