Varignon’s Theorem

Varignon’s Theorem states that the moment of a force about any point is equal to the algebraic sum of the moments of its components about that point.

Principal of moments states that the moment of the resultant of a number of forces about any point is equal to the algebraic sum of the moments of all the forces of the system about the same point.

A theorem in mechanics that establishes the dependence between moments of forces of a given system and the moment of their resultant force. This theorem was first formulated and proved by the French scientist P. Varignon.

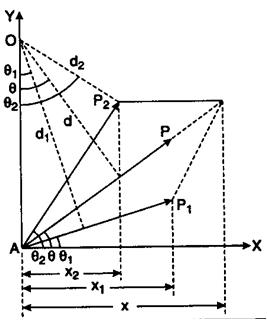
According to Varignon’s theorem, if a system of forces F_i has a resultant force R, then the moment M₀(R) of the resultant force relative to any center O (or z-axis) is equal to the sum of the moments M₀(F_i) of the component forces relative to the same center O (or the same z-axis). Mathematically, Varignon’s theorem isexpressed by the formulas

M₀(R) =ΣM₀(F_i)

or

M_z(R) =ΣM_z(F_i)

Varignon’s theorem is used for solving a series of problems in mechanics (especially statics), resistance of materials, construction theories,and other areas.

Method to solve problems;

The moment of force 100 N about O, can also be determined by using Varignon’s principle. The force 100 N is replaced by its two rectangular components at any convenient point. Here the convenient point is chosen as C. The horizontal and vertical components of force 100 N acting at C are shown in Fig.

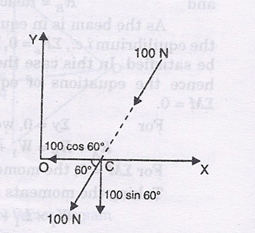
(i) The horizontal component

= 100 × cos 60° = 50 N

But this force is passing through O and hence has no moment about O.

The vertical component

= 100 × sin 60° =-100 × 0.866 = 86.6 N

This force is acting vertically downwards at C. Moment of this force about O

=86.6 × OC = 86.6 × 3

= 259.8 N (clockwise). Ans.

Feedback is important to us.