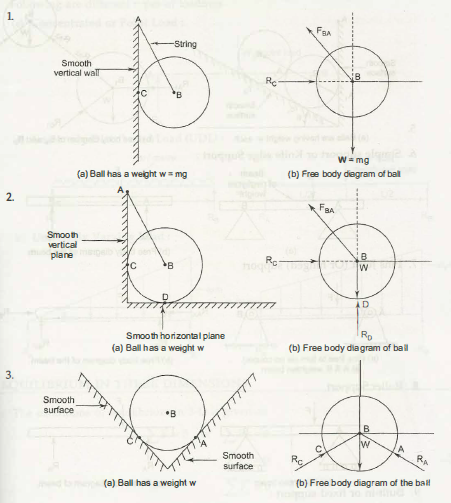
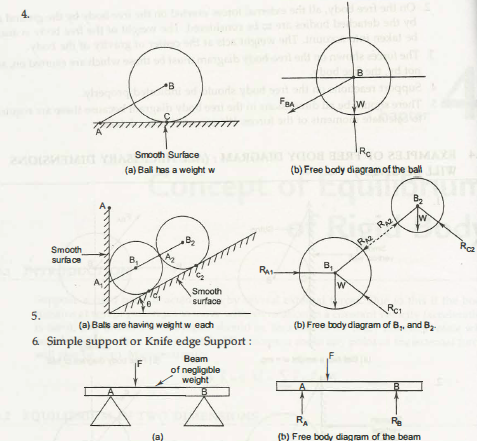
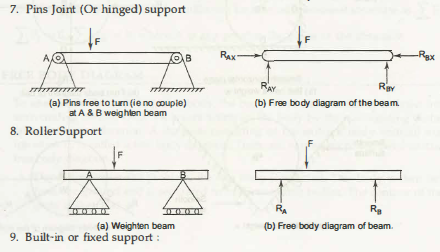
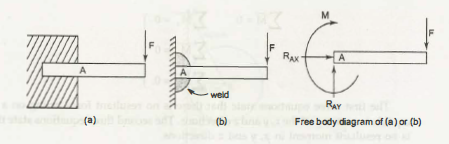
What is a Free Body Diagram Notes pdf ppt

What is a Free Body Diagram:

To analyse the forces acting on a body, the body is to be mechanically isolated from all surrounding bodies. Only the forces acting on the body by the surrounding bodies are taken into consideration. A diagram consisting of the isolated body with all external forces on it, is called a free body diagram.

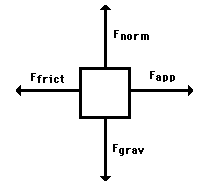
There are various steps followed in drawing free body diagram.

1. Depending upon the problem, the free body is selected. This body is then isolated from the ground and is separated from surrounding bodies. The contour of the free body is sketched.
2.  On the free body, all the external forces exerted on the free body by the ground and by the  detached bodies are to be considered. The weight of the free body is  also to be taken into account. The weight acts at the center of gravity of the body
3.  The forces shown on the free-body diagram must be those which are exerted on, and not by, the free body.
4.  Support reactions on the free body should be indicated properly.
5.  There should be all dimensions in the free body diagram because these are required to calculate moments of the forces. We c.an omit other details.

Problem 2.9. Two smooth circular cylinders, each of weight W = 1000 N and radius 15 cm are connected at their centres by a string AB of length = 40 cm and rest upon a horizontal plane, supporting above them a third cylinder of weight = 2000 N and radius 15 cm as shown in Fig.2.10. Find the force S in the string AB and the pressure produced on the floor at the points of contact D and E.

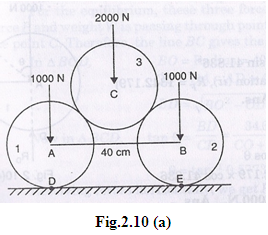
Sol. Given:

Weight of cylinders 1 and 2 = 1000 N

Weight of cylinder 3 = 2000 N
Radius of each cylinder = 15 cm

Length of string AB = 40 cm

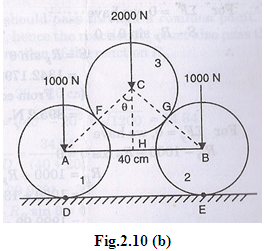
From Fig. 2.10 (b), AC = AF + FC = 15 + 15 = 30 cm

 

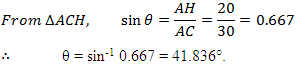
Equilibrium of Cylinder 3:

The cylinder 3 has points of contact at F and G. The reactions RF and Ra will pass through the centre of sphere 3. The free-body diagram is shown in Fig. 2.10(c). Resolving forces horizontally,

RF sin θ – RG sin θ = 0
or RF = RG … (i)
Resolving forces vertically,
RF cos θ + RG cos θ = 2000
or RF cos θ + RG cos θ = 2000 RF = RG)

Equilibrium of Cylinder 1.

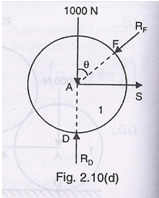
The cylinder 1 has points of contact at D and F. Also the cylinder 1 is connected to cylinder 2 by a string AB. To draw the free-body diagram of cylinder 1, there will be reactions R_F and R_D at points F and D as shown in Fig.2.9 (d). Also there will be a force S in the direction of the string AB.

   For F_x= 0, we have
S -R_F sin θ = 0

S = R_F sin θ

= 1342.179 x sin 41.836°

[ From equation (ii), R_F = 1342.179)
= 895.2 N. Ans.

For F_y= 0, we have

 R_D – 1000 – R_F cos θ = 0

R_D = 1000 + R_F cos θ

= 1000 + 1342.179 × cos 41.836

= 1999.99 = 2000 N. Ans.

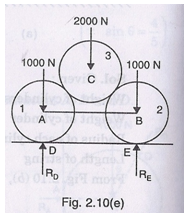
The Equilibrium of Cylinders 1, 2 and 3 Taken Together.

The three cylinders taken together have points of contact at D and E. The free-body diagram is shown in Fig. 2.9 (e). In this case only vertical forces exist. Hence resultant force in y-direction should be zero.

R_D + R_E – 1000 – 2000 -1000 = 0

or   R_E = 1000 + 2000 + 1000 – R_D
R_E = 4000 – R_D

= 4000 – 2000                                          ( R_D = 2000)

=2000 N. Ans. 

EXAMPLES OF FREE BODY DIAGRAM :  

                                                              (ALL NECESSARY   DIMENSIONS WILL BE GIVEN)

 

Feedback is important to us.