D’Alembert’s principle:
Introduction:
D’Alembert’s principle in mechanics, principle permitting the reduction of a problem in dynamics to one in statics. This is accomplished by introducing a fictitious force equal in magnitude to the product of the mass of the body and its acceleration, and directed opposite to the acceleration. The result is a condition of kinetic equilibrium . The principle shows that Newton’s third law of motion applies to bodies free to move as well as to stationary bodies.
Statement of D’Alembert’s principle:
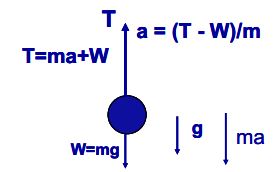
The principle states that the resultant of the external forces and the kinetic reaction acting on a body equals zero. The kinetic reaction is defined as the negative of the product of the mass m and the acceleration a . The principle is therefore stated as F – m a = 0. While D’Alembert’s principle is merely another way of writing Newton’s second law, it has the advantage of changing a problem in kinetics into a problem in statics.
The techniques used in solving statics problems may then provide relatively simple solutions to some problems in dynamics; D’Alembert’s principle is especially useful in problems involving constraints. Thus, in symbols d’Alembert’s principle is,
where
Derivation:
Consider Newton’s law for a system of particles, i. The total force on each particle is
where
Moving the inertial forces to the left gives an expression that can be considered to represent quasi-static equilibrium, but which is really just a small algebraic manipulation of Newton’s law:
Considering the virtual work, δW, done by the total and inertial forces together through an arbitrary virtual displacement, 
, of the system leads to a zero identity, since the forces involved sum to zero for each particle.
At this point it should be noted that the original vector equation could be recovered by recognizing that the work expression must hold for arbitrary displacements. Separating the total forces into applied forces, 
, and constraint forces, 
, yields
If arbitrary virtual displacements are assumed to be in directions that are orthogonal to the constraint forces, the constraint forces do no work. Such displacements are said to be consistent with the constraints.
This leads to the formulation of d’Alembert’s principle, which states that the difference of applied forces and inertial forces for a dynamic system does no virtual work:
