What is Polar Moment of Inertia: Notes pdf ppt Engineering Mechanics

Moment of Inertia Definition:

The concept of moment of inertia was introduced by Leonhard Euler. The resistance that is shown by the object to change its rotation is called moment of inertia. I and J are used as symbols for denoting moment of inertia.The moment of inertia describes the angular acceleration produced by an applied torque. It depends on the shape and mass distribution of the body, and on the orientation of the rotational axis.

The moment of inertia plays the same role for rotation as the mass does for a translational motion, it describes the resistance of a body to a change of its state of motion. The difficulty faced to change the angular motion of any object about an axis is shown or given or measured by calculating moment of inertia about that particular axis.

Moment of Inertia Tensor:

The quantity which allows us to calculate moment of inertia about arbitrary axes like z, etc., is called Moment of Inertia. It is denoted by a matrix I with components shown as below:

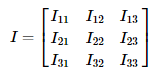
Where,

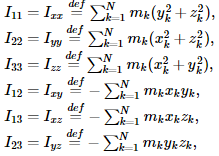
Polar Moment of Inertia Rectangle:

For a rectangle

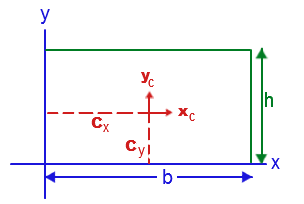
Moment of Inertia Table:

The moment of inertia of a table would be the same as the moment of inertia of rectangle for different axis of rotation. It would be calculated in the same manner as explained above.  through the center as axis of rotation where a and b are tables measurements

Moment of Inertia Equation:

Moment of inertia is given by the following equation,

Here r_i is the distance to the axis on which rotation is done to any other point and not distance of the point to the origin.

Similarly, if we replace the summation by integral then we can find the moment of inertia of a continuous solid body rotating about a particular known axis,

where,
r = Radius vector
P (r ) = Mass density
d (r ) = Distance from a given point r to the known axis of rotation.

First Moment of Inertia:

The first moment of inertia means the moment arm would be raised to a power of one. Hence the first moment of any area calculated about x-axis would be given by

Similarly, the first moment of inertia about y-axis would be given by,

Second Moment of Inertia:

The moment of inertia calculated for an area is called the second moment of inertia. Here the moment arm is raised to a power of 2. Hence the second moment of any area calculated about x-axis would be given by

Similarly, the second moment of inertia about y-axis would be given by

Polar Moment of Inertia:

The polar moment of inertia is related to an axis which is basically perpendicular to the plane of an area. If all of the area is assumed to comprise infinitely small areas da then the polar moment of inertia is the sum of all of these areas x r².

The polar moment of inertia is given b

where,
r = the radius of small area, da from the perpendicular axis – for a plane area the perpendicular axis is a point

The polar moment of inertia is the sum of any two moments of inertia about axes at right angles to each other, e.g.

where,
I_xx gives the moment of Inertia in x-axis
I_yy gives the moment of inertia in y-axis

The polar moment of inertia J of an element about an axis perpendicular to its plane is the product of the area of the element and the square of its distance from the axis. This can also be thought of as the moment of inertia about the Z-axis.

The polar moment of inertia is,

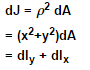
The moment of inertia is that property of a body which makes it reluctant to speed up or slow down in a rotational number

 

Feedback is important to us.