What is Momentum?
The momentum is the stored force which contains by the body in its state of motion. The conservation of momentum states that there is no change in total momentum of system during any change in the system. The body maintained its constant value. Thus, we can say that the momentum of a moving body retains its momentum constant without any external force. It can also be conserved by changing one form of momentum to another form. The momentum related to mass and velocity of the object.
Principle of Conservation of Linear Momentum:
The conservation of linear momentum is based on the principle of Newton’s first law of motion. It implies that for an isolated system, i.e., for a system with no external force, the momentum remains a constant quantity.
It also implies the Newton’s third law of motion, i.e., the law of reciprocal actions which states that the force acting between systems is opposite in sign and equal to each other.
Law of Conservation of Linear Momentum:
- The law of conservation of linear momentum states that the momentum will remain constant no matter what until and unless any external force comes into action.
- This results into the fact that the center of mass of the system of objects will move with the same or constant velocity unless and until it is being acted upon by external force.
- The Conservation of momentum is mathematically the result of the homogeneity of space, i.e., conservation of momentum implies that the physical laws are independent of the position.
Example: When a gun is fired if we assume that the initial position was at rest and hence the initial momentum to be zero the final momentum should also be zero according to the law of conservation of momentum.
Let us suppose the file cabinet is in the middle of the room, a room with a smooth floor, we give it a push in order to move it close to the wall and before we realize it slams into the wall. It is difficult to stop because it has linear momentum.
Conservation of Linear Momentum Equation:
For two objects with initial masses of m1 and m2 and initial velocity of u1 and u2 with final velocities after collision to be v1 and v2, we can write the law as
![]()
- The vector sum of all the given momenta for a closed system with no external force acting on it remains constant
![]()
- Also Linear momentum of a system of particles for a system of particles with a mass of m1, m2, m3 and so on and a velocity v1, v2, v3 and so on the linear momentum can be expressed as
![]()
For two objects with initial masses of m1 and m2 and initial velocity of u1 and u2 with final velocities after collision to be v1 and v2 we can write the law as
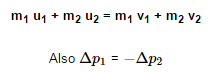
P-The product of mass and the velocity of a particle
![]()
MAGNITUDE:
![]()
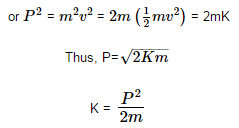
Here, K = kinetic energy.
According to Newton’s second law,
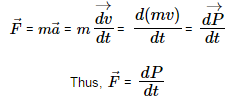
Considering external force on the particle (or a body) = zero,
we have
![]()
The law may be extended to a system of particles or to the center of mass of a system of particles. For example, for system of particles:
If net force (or the vector sum of all the forces) on system of particles = zero, the vector sum of linear momentum of all particles remain conserved:
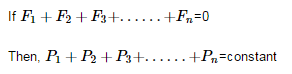
The same is the case for the center of mass
![]()
Conservations of Two Dimensions:
Conservation of linear momentum is also possible in two dimensions by calculating the component of momentum in different axes like x, y and z, also the component of velocity should be calculated in all the axes:
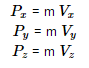
Where![]() are the velocities in x, y and z directions respectively.
are the velocities in x, y and z directions respectively.
